Fórmula de Moivre

Para solucionar esta situación aplicamos la fórmula de Moivre:

Calcula un ángulo “α” (medido en radianes), cuyo coseno:

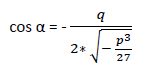
Luego:

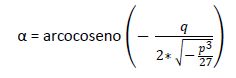
Las raíces de la ecuación son:

Las raíces de la ecuación son:

1ª raíz:

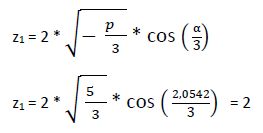
2ª raíz:

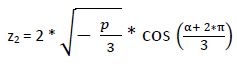
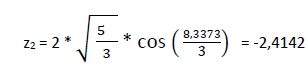
3ª raíz:

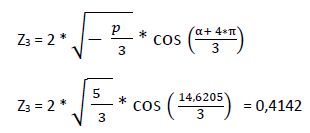
Ya tenemos las 3 soluciones de la ecuación cúbica reducida: las 3 raíces son reales. Ahora tenemos que calcular las soluciones de la ecuación inicial aplicando la conversión:

x = z - 1

Calculamos x1, x2 y x3, que son las soluciones de la ecuación inicial de tercer grado.

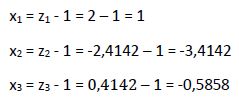
Podemos comprobar como coinciden con las raíces que calculamos al aplicar la Regla de Ruffini.

6º ejemplo

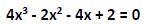
En este ejemplo vamos a aplicar el método Cardano al segundo ejemplo que analizamos con la Regla de Ruffini.

Sustituimos los coeficientes:

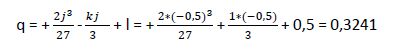
Hacemos un cambio de variable:

Calculamos las tres soluciones de esta ecuación:

1ª Solución:

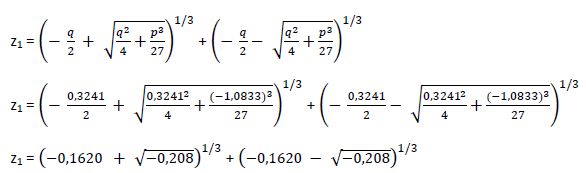
Las raíces cuadradas de números negativos no tienen solución en el conjunto de los números reales. Al igual que en el ejemplo anterior se produce la paradoja de que esta ecuación, que vimos que tenía 3 soluciones reales al aplicar la Regla de Ruffini, no se puede solucionar mediante el método Cardano.

Vamos a aplicar la fórmula de Moivre: calculamos:

Las raíces de la ecuación son:

1° Raíz:

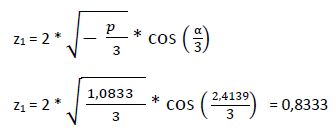
2° Raíz

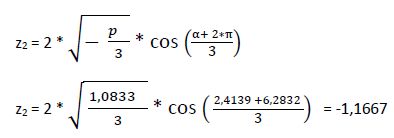
3° Raíz

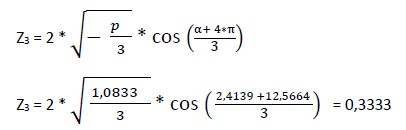
Ya tenemos las 3 soluciones de la ecuación cúbica reducida: las 3 raíces son reales. Ahora tenemos que calcular las soluciones de la ecuación inicial aplicando la conversión:

x = z + 0,1666

Calculamos x1, x2 y x3, que son las soluciones de la ecuación inicial de tercer grado.

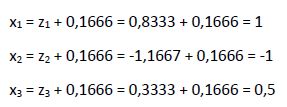
7º ejemplo

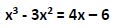
Reordenamos la ecuación, pasando todos sus términos al miembro de la izquierda y ordenando los términos de mayor a menor grado. La ecuación quedaría:

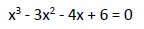
Podemos comprobar como coinciden con las raíces que calculamos al aplicar la Regla de Ruffini.

Sustituimos los coeficientes:

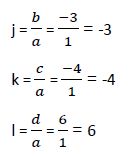
La ecuación queda definida:

Calculamos las tres soluciones de esta ecuación:

1ª Solución:

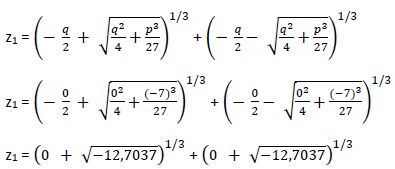
Las raíces cuadradas de números negativos no tienen solución en el conjunto de los números reales.

Vamos a aplicar la fórmula de Moivre: Calculamos:

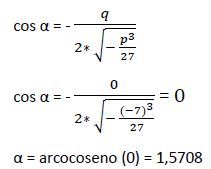
Las raíces de la ecuación son:

1ª raíz:

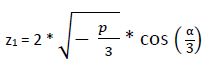
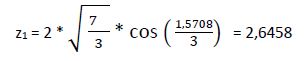
2° Raíz

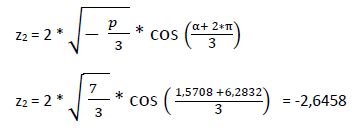
3° Raíz

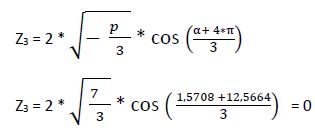
Ya tenemos las 3 soluciones de la ecuación cúbica reducida: las 3 raíces son reales. Ahora tenemos que calcular las soluciones de la ecuación inicial aplicando la conversión:

x = z + 1

Calculamos x1, x2 y x3, que son las soluciones de la ecuación inicial de tercer grado.

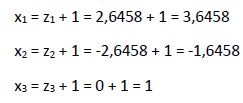
Podemos comprobar como coinciden con las raíces que calculamos al aplicar la Regla de Ruffini.