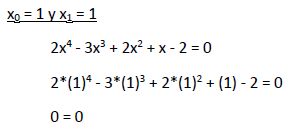Ecuaciones de cuarto grado

Su forma canónica es:

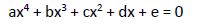
Si algunas de la raíces es un número entero, estas ecuaciones las podremos resolver aplicando la Regla de Ruffini; descomponemos el polinomio en el producto de un factor de primer grado por un factor de tercer grado (que podremos seguir descomponiendo aplicando nuevamente la Regla de Ruffini o, si esto no fuera posible, resolver aplicando el sistema de resolución de ecuaciones de tercer grado).

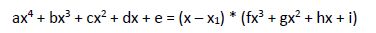
Veamos un par de ejemplos:

1er ejemplo

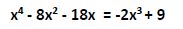
Vamos a escribirla en forma canónica, para ello pasamos todos los términos al miembro de la izquierda y los escribimos de mayor a menor grado.

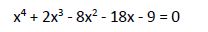
Aplicamos la Regla de Ruffini: probamos con aquellos valores enteros que sean divisores de 9: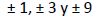 

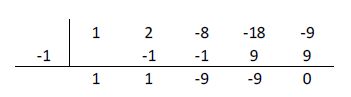
Vemos que cuando x1 = -1 el resto es 0 por lo que es una raíz de esta ecuación, la cual se puede escribir:

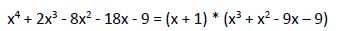
Vamos a tratar de continuar aplicando la Regla de Ruffini con el segundo factor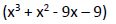 

Por lo tanto, nuevamente cuando x2 = -1 el resto es 0 por lo que es una raíz de esta ecuación.

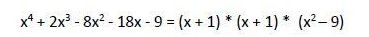
Continuamos aplicando la Regla de Ruffini con el tercer factor:

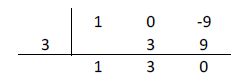
Cuando 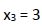 el resto es 0 por lo que es también raíz de esta ecuación.

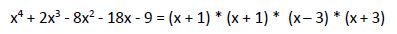
Igualando a 0 el cuarto factor obtendríamos la 4° raíz:

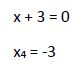
Hemos calculado ya las 4 raíces de la ecuación:

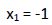
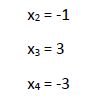
Por último vamos a comprobar que estas cuatro raíces hacen cumplir la igualdad de la ecuación inicial:

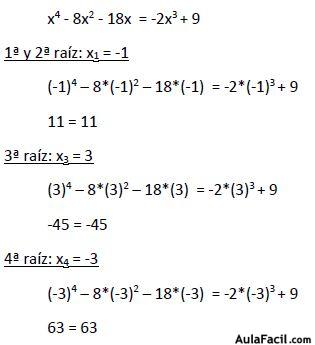
2º ejemplo

(Excel_EGSA2: Hoja 20)

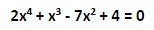
En primer lugar la escribimos en su forma canónica, incluyendo el término de primer grado que falta:

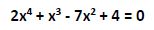
Aplicamos la Regla de Ruffini:

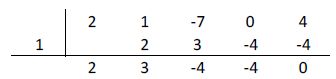
Cuando x1 = 1 el resto es 0 por lo que es una raíz de esta ecuación, la cual se puede escribir:

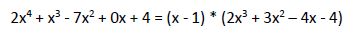
Continuamos aplicando la Regla de Ruffini:

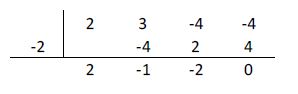
Por lo tanto, nuevamente cuando x2 = -2 el resto es 0 por lo que es una raíz de esta ecuación.

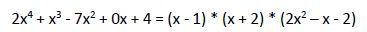
Seguimos aplicando Ruffini con el tercer factor pero no encontramos ningún valor, divisor de 2, que haga que el resto sea 0.

Por lo tanto hemos descompuesto la ecuación en 3 factores, 2 de primer grado (conocemos ya la raíces, x1 = 1 y x2 = -2) y un factor de segundo grado. Para hallar la tercera y la cuarta raíz igualamos este tercer factor a 0 y lo resolvemos aplicando el método de resolución de ecuaciones de segundo grado con una incógnita.

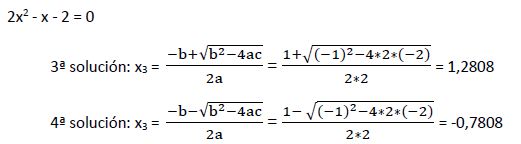
Hemos calculado ya las 4 raíces de la ecuación:

x1 = 1

x2 = -2

x3 = 1,2808

x4 = -0,7808

Por último vamos a comprobar que estas cuatro raíces hacen cumplir la igualdad de la ecuación inicial:

3er ejemplo

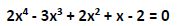
Utilizamos el teorema del resto y la regla de Ruffini. Vamos probando con aquellos valores que sean divisores del término independiente: ±1, ±2

(Excel_EGSA2: Hoja 2)

El resto es 0 por lo que x0 = 1 es una raíz de la ecuación.

Por lo tanto podemos descomponer la ecuación anterior en:

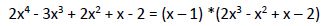
Vamos a tratar seguir descomponiendo la ecuación 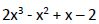 aplicando la regla de Ruffini. Probamos con aquellos valores que sean divisores del término independiente: ±1, ±2 pero tras probar no obtenemos en ningún caso un resto 0 por lo que no podemos continuar con esta descomposición.

El factor (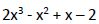) lo podemos igualar a 0 y calcularle sus raíces tal como vimos anteriormente.

Los coeficientes son:

a = 2

b = -1

c = 1

d = -2

Calculamos j, k y l:

j = b / a = -1 / 2 = -0,5

k = c / a = 1 / 2 = 0,5

l = d / a = -2 / 2 = -1

Calculamos p y q:

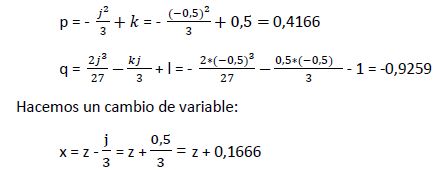
La ecuación inicial queda:

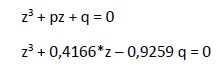
Ya podemos calcular las distintas raíces:

Procedemos a calcular los valores de x que son raíces de la ecuación:

Por lo tanto hemos calculado 2 raíces de la ecuación que son iguales:

x0 = 1

x1 = 1

Vamos a verificar que cumple la igualdad de la ecuación: