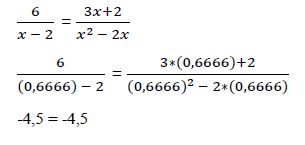Ecuación polinómica racional
La ecuación polinómica racional es aquella ecuación que contiene fracciones polinómicas, es decir, fracciones en las que figura la incógnita en el denominador:
La ecuación polinómica racional tiene la forma:
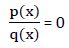
Siendo p(x) y q(x) dos polinomios.
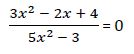
Un método para resolver este tipo de ecuaciones es hallar fracciones equivalentes en las que todas tengan el mismo denominador de forma que podamos eliminar los denominadores.
Ejemplo 1º
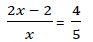
Hallamos fracciones equivalentes con el mismo denominador:
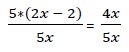
Como ambas fracciones tienen el mismo denominador, estos se pueden eliminar, quedando:
10x – 10 = 4x
Y resolvemos como una ecuación polinómica:
6x = 10
x = 10 / 6
x1 = 1,6666
Una vez calculada la solución tenemos que comprobar 2 cosas:
a) Qué cumple la condición de existencia: es decir, que la solución calculada no haga cero el denominador de ninguna de las fracciones en las que figura la incógnita (una fracción con denominador 0 no tiene solución ya que toma valor ∞).
En el ejemplo:
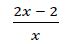
Calculamos los valores que hacen 0 el denominador:
X = 0
Comprobamos que la solución calculada (x1 = 1,6666) es ≠ 0
b) Verificamos que la solución calculada hace cumplir la igualdad de la ecuación. Ya que con las transformaciones realizadas podemos hallar una raíz que no cumpla la igualdad de la ecuación inicial y por lo tanto no sea solución de la misma.
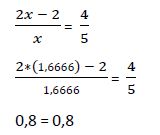
Si una solución calculada no hace cumplir la igualdad en la ecuación original decimos que se trata de una solución extraña. Realmente no es una solución, de ahí la importancia de comprobar que las soluciones calculadas sí funcionan en la ecuación original.
Ejemplo 2º
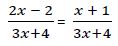
Como ambas fracciones tienen el mismo denominador, estos se pueden eliminar, quedando:
2x – 2 = x + 1
Resolvemos como una ecuación polinómica:
2x – 2 = x + 1
2x – x = 1 + 2
x1 = 3
a) Comprobamos que cumple la condición de existencia:
Calculamos los valores que hacen 0 los denominadores donde figura la incógnita:
3x + 4 = 0
3x = -4
x = -4 / 3 = -1,3333
La solución calculada (x1 = 3) es ≠ -1,3333
b) Verificamos que la solución calculada hace cumplir la igualdad de la ecuación.
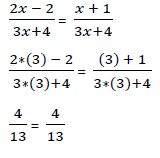
Ejemplo 3º
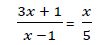
Calculamos fracciones equivalentes con el mismo denominador. El denominador común de ambas fracciones será el producto de los denominadores: 5 * (x – 1)
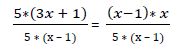
Al ser iguales los denominadores podemos eliminarlos:
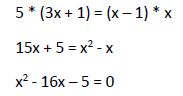
Esta ecuación la podemos resolver aplicando el método de resolución de ecuaciones de segundo grado con una incógnita.
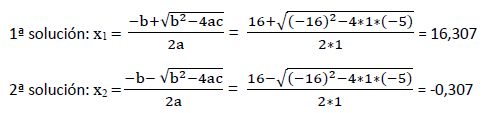
a) Comprobamos que las soluciones cumplen la condición de existencia:
Calculamos los valores que hacen 0 los denominadores donde figura la incógnita:
x – 1 = 0
x = 1
Las soluciones calculadas (x1 = 16,307 y x2 = -0,307) son ≠ 1
b) Comprobamos en la ecuación inicial si estas soluciones hacen cumplir la igualdad:
1ª solución:
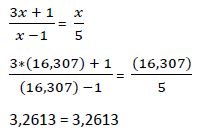
2ª solución
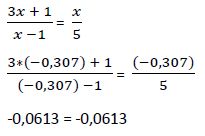
Ejemplo 4º
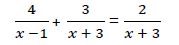
Calculamos fracciones equivalentes con el mismo denominador. El denominador común de estas fracciones es el producto: (x – 1) * (x + 3)
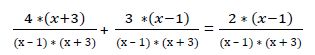
Al ser iguales los denominadores podemos eliminarlos:
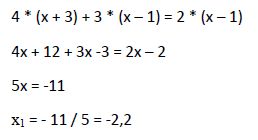
a) Comprobamos que la solución cumple la condición de existencia:
Calculamos los valores que hacen 0 a los denominadores donde figura la incógnita:
x – 1 = 0, luego x = 1
x + 3 = 0, luego x = -3
La solución calculada (x1 = -2,2) es ≠ 1 y es ≠ -3
b) Comprobamos si en la ecuación inicial esta solución hace cumplir la igualdad:
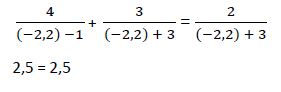
Ejemplo 5º
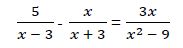
Calculamos fracciones equivalentes con el mismo denominador.
Sabemos que:
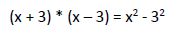
El denominador común de estas fracciones es: 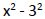
Por lo tanto:
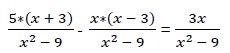
Al ser iguales los denominadores podemos eliminarlos, quedando:
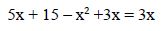
Operamos:
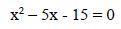
Esta ecuación la podemos resolver aplicando el método de resolución de ecuaciones de segundo grado con una incógnita.
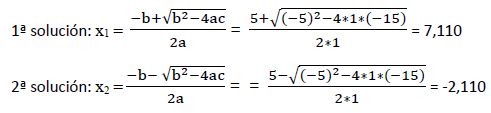
a) Comprobamos que las soluciones cumplen la condición de existencia:
Calculamos los valores que hacen 0 los denominadores donde figura la incógnita:
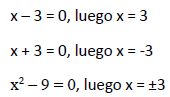
Las soluciones calculadas (x1 = 7,110 y x2 = -2,110) son ≠ ±3
b) Comprobamos en la ecuación inicial si estas soluciones hacen cumplir la igualdad:
1ª solución:
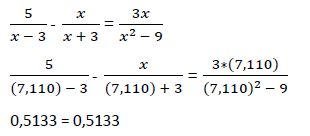
2ª solución:
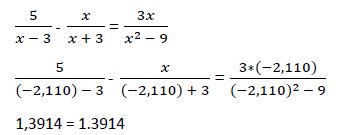
Las dos soluciones calculadas hacen cumplir la igualdad en la ecuación original, por lo que son efectivamente soluciones de estas.
Ejemplo 6º
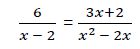
El denominador del miembro de la derecha se puede expresar:
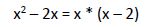
Calculamos fracciones equivalentes con el mismo denominador.
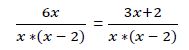
Como los denominadores son iguales podemos eliminarlos. La ecuación quedaría:
6x = 3x + 2
Operamos:
6x - 3x = 2
3x = 2
x1 = 2 / 3 = 0,6666
a) Comprobamos que la solución cumple la condición de existencia:
Calculamos los valores que hacen 0 los denominadores donde figura la incógnita:
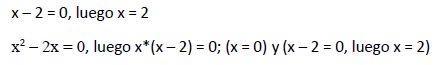
La solución calculada (x1 = 0,6666) es ≠ 2 y es ≠ 0
b) Tenemos que comprobar que en la ecuación inicial hace cumplir la igualdad: