Ecuación polinómica racional II
Ejemplo 7º
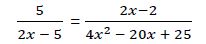
El denominador del miembro de la derecha se puede expresar:
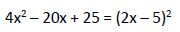
La ecuación inicial se puede escribir:
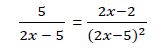
Calculamos fracciones equivalentes con el mismo denominador.
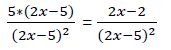
Al ser iguales los denominadores podemos eliminarlos. La ecuación quedaría:
5*(2x – 5) = 2x - 2
Operamos:
10x - 25 = 2x - 2
8x = 23
x1 = 23 / 8 = 2,875
a) Comprobamos que la solución cumple la condición de existencia:
Vimos que el denominador de la fracción del miembro de la derecha se puede escribir:
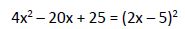
Calculamos los valores que hacen 0 este denominador:
2x – 5 = 0, luego x = 2,5
La solución calculada (x1 = 2,875) es ≠ 2,5
b) Tenemos que comprobar que en la ecuación inicial hace cumplir la igualdad:
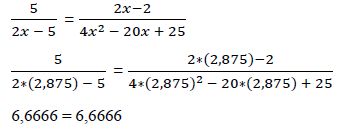
Ejemplo 8º
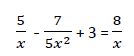
El denominador común de estas fracciones es 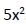 . Calculamos una ecuación equivalente en la que todos los términos tengan el mismo denominador:
. Calculamos una ecuación equivalente en la que todos los términos tengan el mismo denominador:
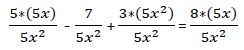
La ecuación quedaría:
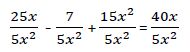
Al ser iguales los denominadores podemos eliminarlos.
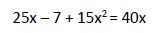
Se trata de una ecuación de segundo grado con una incógnita. La escribimos en su forma canónica, para ello pasamos todos los términos al miembro de la izquierda y los ordenamos de mayor a menor grado.
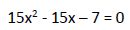
Resolvemos esta ecuación aplicando el método de resolución de ecuaciones de segundo grado con una incógnita:
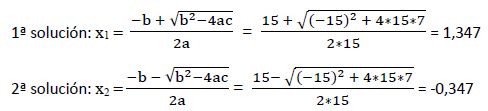
a) Comprobamos que las soluciones cumplen la condición de existencia:
Calculamos los valores que hacen 0 este denominador:

Las soluciones calculadas (x1 = 1,347 y x2 = -0,347) son ≠ 0
b) Tenemos que comprobar que en la ecuación inicial hacen cumplir la igualdad:
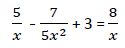
1ª Raíz: x1 = 1,347
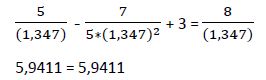
2ª Raíz: x1 = -0,347
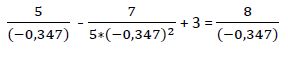
-23,0839 = -23,0839
Ejemplo 9º
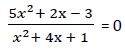
Esta ecuación valdrá 0 cuando el numerador sea igual a 0.
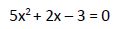
Resolvemos esta ecuación aplicando el método de resolución de ecuaciones de segundo grado con una incógnita:
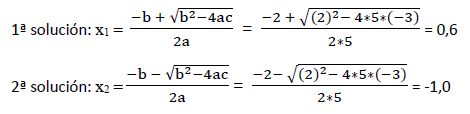
a) Comprobamos que la solución cumple la condición de existencia:
Calculamos los valores que hacen 0 el denominador:
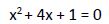
Resolvemos esta ecuación aplicando el método de resolución de ecuaciones de segundo grado con una incógnita:
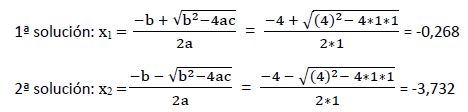
Las soluciones calculadas (x1 = 0,6 y x2 = -1,0) son ≠ -0,268 y son ≠ -3,732
b) Tenemos que comprobar que en la ecuación inicial hacen cumplir la igualdad:
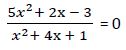
1ª Raíz: x1 = 0,6
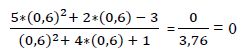
2ª Raíz: x1 = -1,0
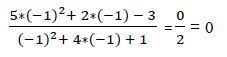
Ejemplo 10º
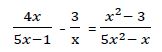
El denominador de la ecuación del miembro de la derecha lo podemos descomponer:
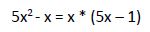
La ecuación la podemos escribir:
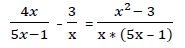
Calculamos fracciones equivalentes en las que todas tengan el mismo denominador:
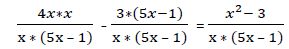
Ya podemos prescindir de los denominadores:
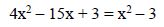
Operamos para escribir esta ecuación de segundo grado con una incógnita en su forma canónica:
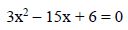
Resolvemos:
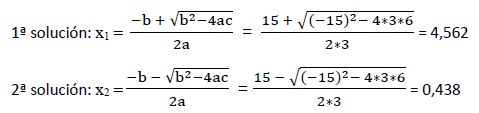
a) Comprobamos que la solución cumple la condición de existencia:
Calculamos los valores que hacen a 0 los denominadores:

Las soluciones calculadas (x1 = 4,562 y x2 = 0,438) son ≠ 0,2 y son ≠ 0
b) Tenemos que comprobar que en la ecuación inicial hacen cumplir la igualdad:
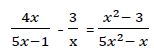
1ª Raíz: x1 = 4,562
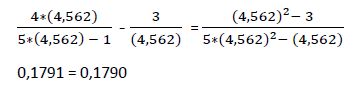
2ª Raíz: x2 = 0,438
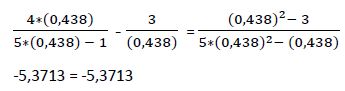
Ejemplo 11º
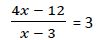
Calculamos fracciones equivalentes en la que todas tengan el mismo denominador:
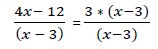
Ya podemos prescindir de los denominadores:
4x - 12 = 3x - 9
Operamos:
4x – 3x = -9 + 12
x1 = 3
a) Comprobamos que la solución cumple la condición de existencia:
Calculamos los valores que hacen 0 a los denominadores:
x – 3 = 0, luego x = 3
El valor que hacer 0 el denominador coincide con la solución calculada, luego esta solución no es válida.
Podemos comprobarlo calculando el valor de la ecuación cuando x1 = 3
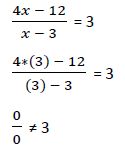
La fracción 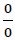 no tiene solución.
no tiene solución.


