Ecuación logarítmica
La ecuación logarítmica entra dentro del grupo de ecuaciones no polinómicas. En ellas la incógnita figura dentro de un logaritmo.
Veamos algunos ejemplos:
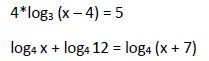
Para resolver estas ecuaciones hay que operar usando logaritmos. Por ello vamos a comenzar repasando las propiedades de los logaritmos.
Propiedades de los logaritmos
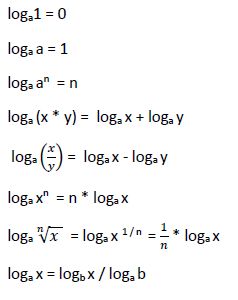
Resolución de ecuaciones logarítmicas
Ejemplo 1º
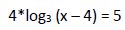
Comenzamos simplificando:
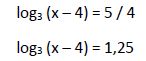
Resolvemos el logaritmo:
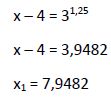
Una vez calculada la raíz de la ecuación hay que comprobar que hace cumplir la igualdad de la ecuación inicial, no originando ningún logaritmo nulo o negativo (ya que estos logaritmos no existen):
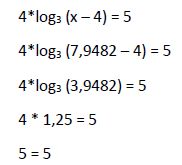
Por tanto, la solución calculada (x1 = 7,9482) es solución válida de la ecuación inicial.
Ejemplo 2º

Una vez calculada la raíz de la ecuación hay que comprobar que haga cumplir la igualdad de la ecuación inicial, no originando ningún logaritmo nulo o negativo:
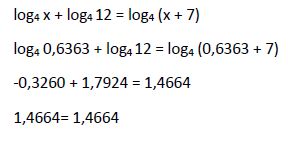
Por tanto, la solución calculada (x1 = 0,6363) es solución válida de la ecuación inicial.
Ejemplo 3º

Resolvemos aplicando el método de resolución de las ecuaciones de segundo grado con una incógnita:
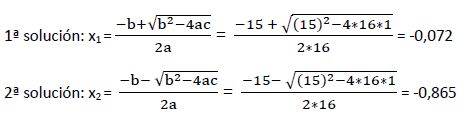
Una vez calculada la raíz de la ecuación hay que comprobar que haga cumplir la igualdad de la ecuación inicial, no originando ningún logaritmo nulo o negativo:
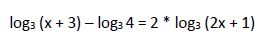
1ª solución: x1 = -0,072
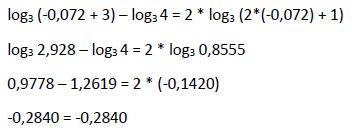
Por lo tanto, esta solución sí es una solución válida de la ecuación inicial.
2ª solución: x2 = -0,865
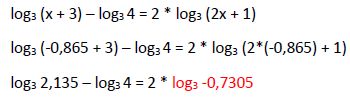
El término del miembro de la derecha 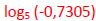 es un logaritmo negativo que no existe por lo que esta solución no es una solución válida de la ecuación inicial.
es un logaritmo negativo que no existe por lo que esta solución no es una solución válida de la ecuación inicial.
Ejemplo 4º

Resolvemos aplicando el método de resolución de las ecuaciones de segundo grado con una incógnita:
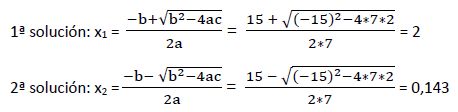
Una vez calculada la raíz de la ecuación hay que comprobar que haga cumplir la igualdad de la ecuación inicial, no originando ningún logaritmo nulo o negativo:
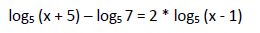
1ª solución: x1 = 2

Por lo tanto, la primera solución (x1 = 2) es solución de la ecuación inicial.
2ª solución: x2 = 0,143
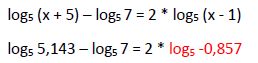
El término del miembro de la derecha 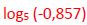 es un logaritmo negativo que no existe por lo que esta solución no es una solución válida de la ecuación inicial.
es un logaritmo negativo que no existe por lo que esta solución no es una solución válida de la ecuación inicial.
Ejemplo 5º

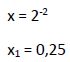
Una vez calculada la raíz de la ecuación hay que comprobar que haga cumplir la igualdad de la ecuación inicial, no originando ningún logaritmo nulo o negativo:
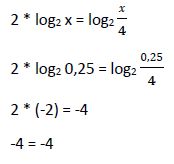
Por lo tanto la solución x1 = 0,25 es solución válida de la ecuación inicial.
Ejemplo 6º

Una vez calculada la raíz de la ecuación hay que comprobar que haga cumplir la igualdad de la ecuación inicial, no originando ningún logaritmo nulo o negativo:
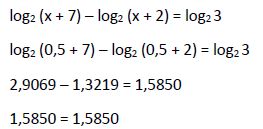
Por lo tanto la solución x1 = 0,5 es solución válida de la ecuación inicial.
Ejemplo 7º

Resolvemos la ecuación aplicando el método de resolución de las ecuaciones de segundo grado con una incógnita:
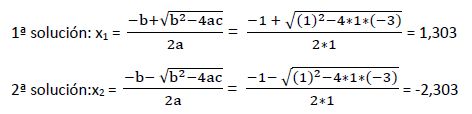
Una vez calculada la raíz de la ecuación hay que comprobar que haga cumplir la igualdad de la ecuación inicial, no originando ningún logaritmo nulo o negativo:
1ª solución: x1 = 1,303
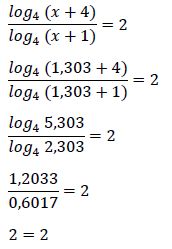
Por lo tanto la solución x1 = 1,303 es solución válida de la ecuación inicial.
2ª solución: x2 = -2,303
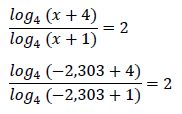
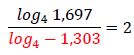
El logaritmo del denominador es negativo por lo que no se puede resolver. Por tanto la solución x2 = -2,303 no es una solución válida de la ecuación inicial.


