Trabajo con Fuerza Variable

Comenzamos este apartado tomando buena nota de cuanto acabamos de escribir en el RESUMEN.

En el gráfico siguiente observamos con color amarillo la trayectoria recorrida por un móvil.

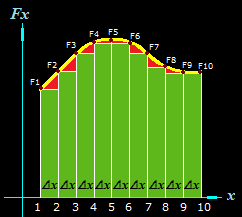
Esta trayectoria curva vemos que está compuesta de diversos puntos.

Cada punto significa el valor de la Fuerza con relación a la posición de desplazamiento (valor de x).

Por ejemplo, cuando el objeto se ha desplazado 1m (eje de abscisas) es porque le hemos aplicado una Fuerza F1. En el desplazamiento del objeto desde el primer metro hasta el segundo hemos aplicado una Fuerza F2, etc.

Queda claro que ahora la Fuerza que aplicamos al objeto no es constante, va variando.

Si sumamos las áreas de todos los rectángulos donde las bases son iguales (Δx), en cambio, las alturas son diferentes pues representan a los valores de las Fuerzas, el área obtenida de esta suma no es igual al área bajo la curva porque a las zonas en color rojo no las hemos tenido en cuenta.

Imagina que las distancias en lugar de 1m son de medio metro:

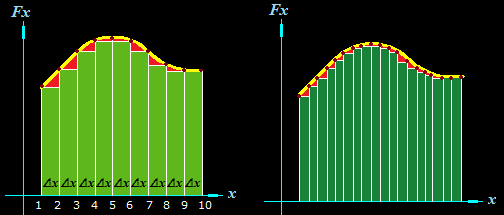
Notarás que en la figura de la derecha el valor de Δx ha decrecido y esto hace que el número de rectángulos ha aumentado y que la suma de las áreas de éstos aunque sigue siendo “parecida” a la obtenida anteriormente, es un poco mayor debido a que la superficie de las zonas en rojo ha decrecido.

Si los rectángulos aumentan en número al reducir el valor de Δx, llegará un momento en el que las zonas rojas desaparecen:

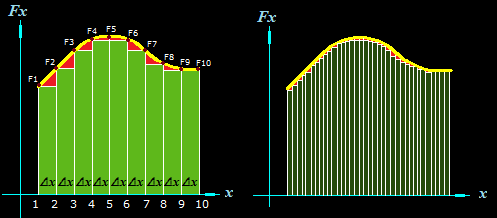
En la figura de la derecha ha aumentado el número de sumandos, es decir, ha crecido el número de áreas de rectángulos y la suma de todas estas áreas se acerca más al área bajo la curva.

Si comparas las dos figuras notarás que la zona relativa a las áreas en rojo ha decrecido.

¿Qué haremos para que las áreas en rojo desaparezcan?

Sencillamente, reducir el valor de Δx, o lo que es lo mismo, aumentar el número de rectángulos y para esto, hacemos que Δx tienda a .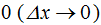

Sumar las infinitas áreas lo conseguimos utilizando las integrales.

La base de cada rectángulo (todas iguales) están representadas por la diferencial x: dx y la altura de cada rectángulo está en función del valor de x (F_x):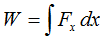 

Pero hemos de indicar en la fórmula los valores del intervalo, un valor inicial x_i y un valor final x_f para la variable independiente x:

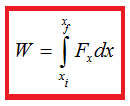
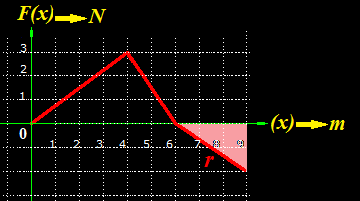
3.17 En la figura siguiente puedes ver desarrollo gráfico del Trabajo realizado por una Fuerza variable sobre un móvil.

Se trata de calcular el Trabajo realizado por la Fuerza cuando el móvil se desplaza:

a) Desde x = 0 hasta x = 4

b) Desde x = 4 hasta x = 6

c) Desde x = 6 hasta x = 9

d) Trabajo Total

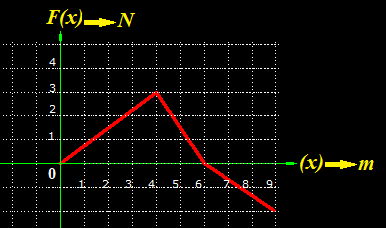
Respuestas: 6J, 3J, -3J, 6J

Solución (a)

Lo resolvemos primeramente teniendo cuenta lo aprendido en Geometría elemental puesto que hemos visto que el Trabajo es el Área de la variable independiente x por la dependiente de x que es F(x). F(x) depende del valor de x.

La recta comprendida entre los puntos 0 y 4 de x vemos que es la base de in triángulo (en azul) cuya área es:

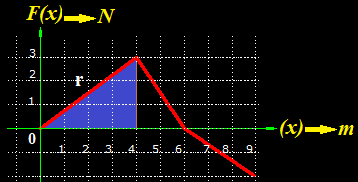
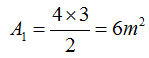
Esta misma área la calculamos por integrales.

Lo primero que hemos de calcular es la ecuación de la recta r.

Conocidos los puntos (0,0) y (4,3) de esta recta hallamos su pendiente m de la ecuación:

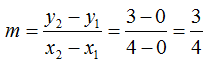
La ecuación de la recta la obtenemos de:

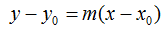
Sustituimos valores y haciendo operaciones llegamos a la ecuación de la recta:

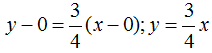
Conocemos la ecuación de la recta y además el valor de la función F_x que es también vale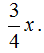  

Integramos la función para calcular el Trabajo y haciendo operaciones paso a paso llegamos a:

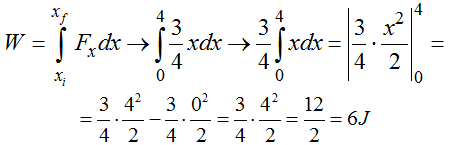
Vemos que el área expresada en m² equivale al Trabajo expresado en J.

Ahora calculamos el área en color verde, geométricamente e integrando:

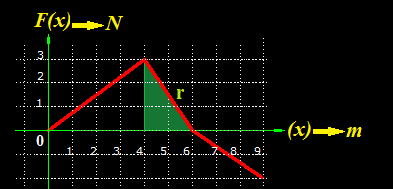
Geométricamente tenemos que la base vale 2m y la altura 3m, el área valdrá: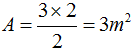 

 
Por integrales calculamos primero la ecuación de la recta r sabiendo que son puntos de la misma (4,3) y (6,0):

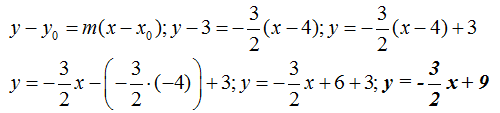
Una vez obtenida la ecuación de la recta la integramos en el intervalo [4,6] y haciendo operaciones paso a paso obtenemos:

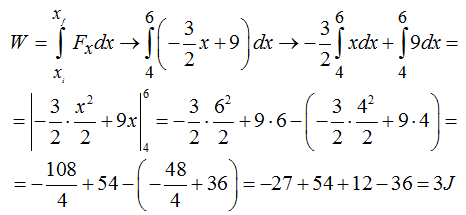
Nos queda por calcular el área del último triángulo (color rojo):

El proceso es el mismo que en los casos anteriores con la salvedad que como la altura (-2m) es negativa por hallarse bajo 0.

El área es: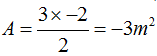  

Calculamos primero la ecuación de la recta teniendo en cuenta los puntos (6,0) y (9,-2):

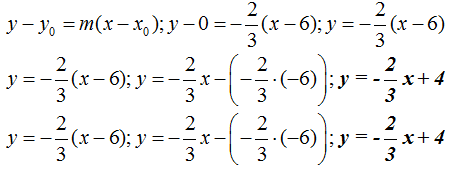
Integramos:

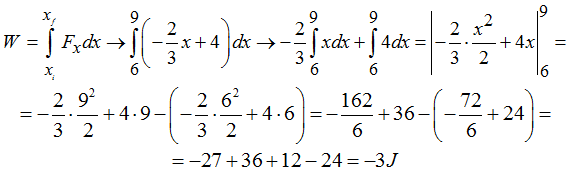
El Trabajo total es: 6J + 3J + (-3J) = 6J