Múltiplos del Vatio
En el cálculo de problemas verás que obtenemos resultados un poco incómodos a la hora de presentar los resultados si los hacemos en vatios.
Los dos múltiplos más utilizados son el kW leemos kilovatio y como su nombre indica, representa a 1000 vatios o 1000W y el Caballo Vapor CV o Horse Power (HP) en inglés: 1 CV equivale a 736 vatios.
Para que tengas una pequeña idea, 1 CV es la potencia necesaria para elevar a 1 m de altura un peso de 75kg en un segundo.
Otra equivalencia (no muy práctica) es la de 1kW = 1,36CV
3.54 En el dibujo siguiente tienes un motor eléctrico con su correspondiente polea que al girar sube un peso de 5kg hasta una altura de 3m en 2 segundos.
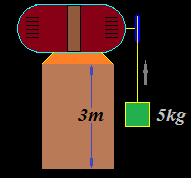
Respuesta: 73,5W
Solución
Basta utilizar la fórmula recientemente estudiada y sustituir en ella los valores que conocemos:
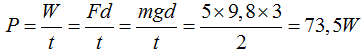
3.55 En las fotografías siguientes:

observas unas ruedas que al girar horizontalmente ponen en movimiento un resistente cable del que cuelgan unas cabinas, o unas sillas que si no has viajado en ellas sí las habrás visto, por si acaso, tienes a continuación una muestra:

El problema que se te propone dice:
Calcula la Potencia que ha de tener el motor para transportar una cabina de 6T de peso colgada de un cable de 5km de longitud y una inclinación de 30º moviéndose a velocidad constante de 10m/s. No tenemos en cuenta el peso del cable ni los rozamientos.
Respuesta: 294kW
Dibujamos en primer lugar el esquema (I):
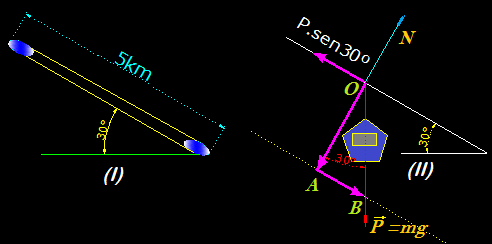
En este esquema tenemos el cable con las dos ruedas que al girar horizontalmente, arrastra al cable que tiene una inclinación de 30º y del que cuelga la cabina.
En el esquema (II) hemos de fijarnos que en el punto del que cuelga la cabina cuyo peso es de 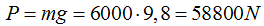 actúan dos Fuerzas que son el Peso de la cabina y la que produce el cable equivalente a su componente paralela al eje x.
actúan dos Fuerzas que son el Peso de la cabina y la que produce el cable equivalente a su componente paralela al eje x.
Al vector 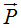 lo descomponemos en la suma de los vectores
lo descomponemos en la suma de los vectores 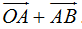 . Nos interesa su componente paralela al eje x debido a que la componente respecto al eje y con el valor de normal (N) se contrarrestan.
. Nos interesa su componente paralela al eje x debido a que la componente respecto al eje y con el valor de normal (N) se contrarrestan.
El valor de 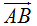 lo calculamos haciendo uso de lo estudiado en Trigonometría:
lo calculamos haciendo uso de lo estudiado en Trigonometría: 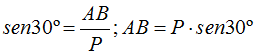 y sustituyendo valores llegamos a:
y sustituyendo valores llegamos a: 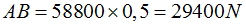
Ahora hallamos el Trabajo que hace la Fuerza de 29400N a lo largo de 5km para conocer la Potencia: 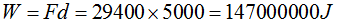
Para saber la Potencia a partir de: 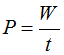 vemos que no tenemos datos sobre el tiempo pero sí conocemos la velocidad de la cabina:
vemos que no tenemos datos sobre el tiempo pero sí conocemos la velocidad de la cabina:
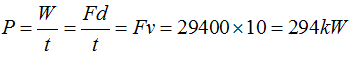
3.56 En la fotografía siguiente tienes un tren de alta velocidad cuyo peso es de 400 Toneladas que marcha a 300km/h. Supongamos que el maquinista recibe un aviso de un desprendimiento de tierra sobre la vía a 4km de distancia.

Acciona el sistema de frenado produciendo una deceleración de 1,1m/s2.
1) ¿Cuál es la Fuerza realizada por el sistema de frenado?
2) ¿Cuánto ha tardado en parar?
3) ¿Evita la colisión?
Respuestas: 1ª) -138877,78N; 2ª) 75,76s; 3ª) 3156,31m(evita la colisión)
Solución
En primer lugar calculamos la velocidad en m/s:
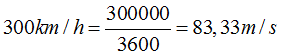
Calculamos la Ec del tren en el momento de recibir el aviso:
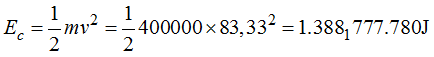
Es el valor que deben conseguir los frenos (con signo negativo) por lo que el Trabajo realizado por éstos es de 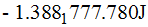 debido a que ΔEc = W.
debido a que ΔEc = W.
Tiempo de frenado:
Va a una velocidad inicial de 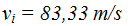
La velocidad final ha de ser 0 para llegar a pararse.
Sabemos que 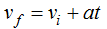 de donde sustituyendo valores que conocemos y despejando t llegamos a:
de donde sustituyendo valores que conocemos y despejando t llegamos a:
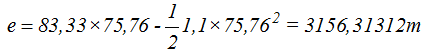
Espacio que necesita para parar:
Conocemos la velocidad inicial, el tiempo y la aceleración hacemos uso de 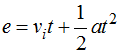 . Sustituimos los valores conocidos teniendo en cuenta que la aceleración es negativa y obtenemos:
. Sustituimos los valores conocidos teniendo en cuenta que la aceleración es negativa y obtenemos:
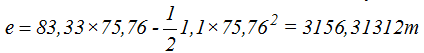
Evita la colisión.
Comentario: Merece la pena destacar el detalle de la cantidad de espacio que necesita un tren AVE (alta velocidad española) para detenerse sin que ningún pasajero resulte dañado. Decimos esto porque es de suponer que podría frenar en un espacio más corto, pero probablemente muchos pasajeros resultarían heridos por caídas en el interior del tren (los que se hallan de pie, caminando por el pasillo, en el bar, maletas que se caen, etc.).

