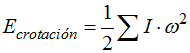Energía Cinética de rotación
Supongamos unas partículas girando alrededor de un eje, cada una en su órbita:
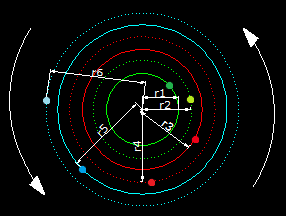
Cada una dista del centro una medida ri tomando i valores desde 1 hasta 6.
La velocidad lineal de cada una es diferente dependiendo de su velocidad angular que será la misma para todas y de su distancia al centro, es decir, del radio: vi =ω . ri
El número de partículas que tiene un cuerpo sólido es infinito y si suponemos que está girando alrededor de un punto significa que son infinitas partículas las que giran.
La suma de las energías de cada partícula girando nos dará la Energía cinética de total del sólido.
Partiendo de la 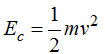 puedo decir que:
puedo decir que:
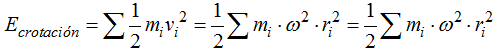
El último término lo puedo escribir:
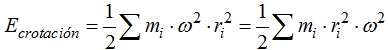 realizo este cambio del orden de los factores porque por lo estudiado en Cinemática sabemos que:
realizo este cambio del orden de los factores porque por lo estudiado en Cinemática sabemos que: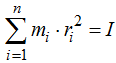 (momento de inercia) y de este modo puedo escribir:
(momento de inercia) y de este modo puedo escribir: