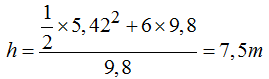Energía potencial asociada a una fuerza conservativa

Volvemos a repetir el concepto del Trabajo (decían los antiguos: “la repetición es la madre de la sabiduría”).

Un cuerpo para trasladarse del punto A al punto B recorre un camino e:

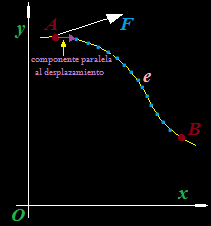
El Trabajo nos viene dado por el producto de la componente paralela de la Fuerza que aplicamos en cada punto del recorrido, multiplicada por la distancia recorrida: W = F . d

Una forma INCORRECTA de calcular el Trabajo sería, sumar todos los productos de F por la distancia que existe entre dos puntos consecutivos. Para que no sea INCORRECTA, los puntos donde aplicamos la Fuerza tendrían que estar pegados unos a otros.

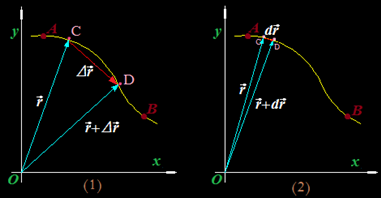
Para ello incrementamos el vector que nos va indicando la posición que ocupa el móvil.

En (1) el incremento de es 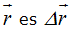vector representado por el vector 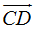(en color rojo) NO corresponde al camino recorrido por el cuerpo.

Aunque el incremento haya sido pequeño, existe una importante diferencia entre 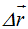y la distancia del camino comprendido entre los puntos C y D.

Para hacer nulas estas diferencias (2) entre el incremento del vector 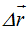y el arco correspondiente del camino e recorrido hacemos que el valor del incremento tienda a 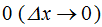con lo que, pasando al cálculo infinitesimal escribimos: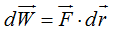 

La suma o integración de los (productos 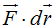 comprendidos entre los puntos A y B) vendrá dada por:

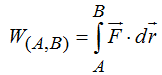
En la figura siguiente:

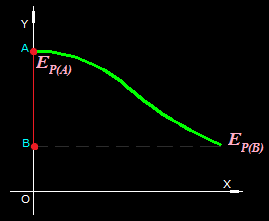
tenemos el camino (en color verde) que recorre un cuerpo sometido a una Fuerza conservativa referido al eje y entre los puntos A y B.

Según lo estudiado anteriormente el Trabajo lo escribimos 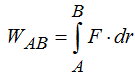 pero ateniendo a lo representado en la figura y tomando como diferencial a la ordenada al mismo tiempo que sustituimos a la Fuerza F por mg (por tratarse de una fuerza conservativa), efectuando operaciones paso a paso tenemos:

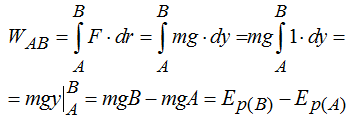
Cuando trabajamos con una fuerza conservativa podemos decir que el Trabajo realizado por ella en el desplazamiento entre los puntos A y B es igual a la diferencia de sus Energías potenciales entre dichos puntos.

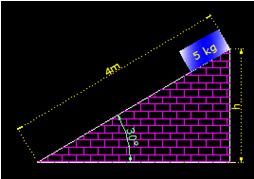
3.33 Un cuerpo de 20kg desciende (partiendo del reposo y sin rozamientos) por un plano inclinado de 30º llegando al final del mismo con una velocidad de 20m/s.

Respuesta: 40,82m

Solución

En primer lugar dibujamos de acuerdo con el contenido del texto:

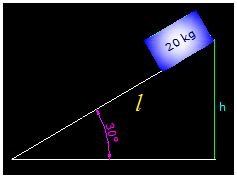
Además de la longitud del plano inclinado desconocemos la altura (h).

Sabemos que cuando en un sistema solamente actúan fuerzas conservativas la E_m se mantiene constante.

h_i a la altura inicial

h_f a la altura al final del deslizamiento

v_i a la velocidad inicial

v_f a la velocidad final

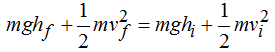
Como la altura final, al llegar al plano horizontal es 0 el primer sumando vale 0, es decir, la E_p vale 0.

La E_c en el punto más alto del plano inclinado vale 0 porque la velocidad es cero.

Teniendo en cuenta lo que acabamos de escribir y sustituyendo valores tenemos: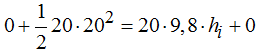 

Despejamos la altura después de simplificar ambos miembros de la igualdad por 20:

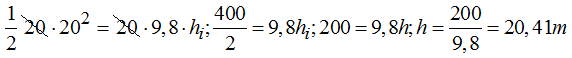
Llamando l a la longitud del plano inclinado tenemos que:

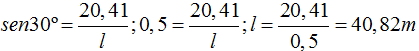
3.34 Con los datos que presenta la siguiente figura, suponiendo que no existe rozamiento y dejando deslizar a la caja ¿con qué velocidad llega al punto más bajo del plano?

Respuesta: 6,26m/s

Solución

No hay más fuerzas que la gravedad.

La E_m es la misma en todos los puntos del plano.

Representamos por: 

h_i a la altura en lo más alto del plano.

h_f a la altura en lo más bajo del plano.

v_i a la velocidad inicial.

v_f a la velocidad final.

La igualdad siguiente nos permite calcular la velocidad de llegada a la parte más baja del plano:

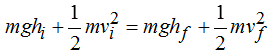
Simplificando por m y sabiendo que la E_c en lo más alto del plano al no haber velocidad es cero lo mismo que su E_p en lo más bajo del plano por no haber altura podemos escribir:

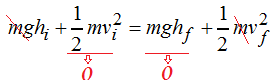
Llegando a la igualdad: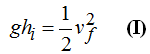 

La altura equivale a: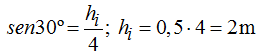 

Sustituimos este valor en (I):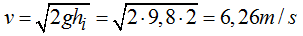  

3.35 Calcula el Trabajo que realizas al subir una caja de 10kg a una altura de 2m sin utilizar ningún plano inclinado y utilizándolo sabiendo que la inclinación es de 30º. No se tienen en cuenta los rozamientos.

1)¿Cuál es la diferencia de los Trabajos realizados en cada caso?

2)¿Cuál es la diferencia de las Fuerzas utilizadas en cada caso?

Respuestas:

1ª) No existen diferencias en cuanto al Trabajo

2ª) Usando el plano inclinado ahorro Fuerza

Solución

Dibujamos la figura correspondiente:

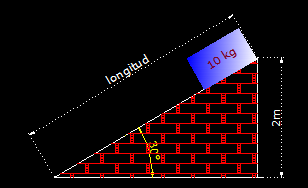
Si no utilizo un plano inclinado el Trabajo es:

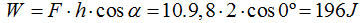
También podría haber calculado el Trabajo basándome en la E_p:

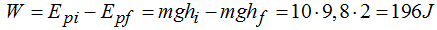
Ahora calculo el Trabajo teniendo en cuenta sus E_c:

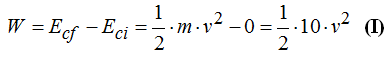
Necesitamos conocer el valor de v:

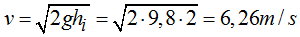
Sustituimos este valor en (I):

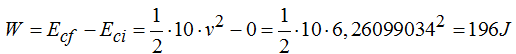
Con plano inclinado o sin él, el Trabajo es el mismo.

La Fuerza sin utilizar el plano es: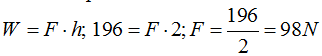 

También podía haberlo calculado: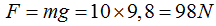 

Utilizando el plano inclinado debo conocer la longitud del mismo que lo represento por l: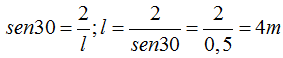 

Deduzco el valor de la F fijándome en la figura siguiente: 

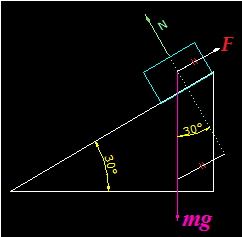
Compruebo que F equivale a: mg.sen 30º = 10 . 9,8 . 0,5 = 49N

Con el plano inclinado hago menos Fuerza, en este caso, la mitad.

3.36 Un tipo de problema que pocas veces falta cuando tratamos el tema del que nos estamos ocupando es el de calcular la altura a la que debe encontrarse un objeto, la bola roja en nuestro caso, de 10kg para que partiendo del reposo tenga la suficiente Energía para describir el bucle vertical de 3m de radio.

¿Cuál es la velocidad a su paso por el punto A?

La figura la representamos del modo siguiente:

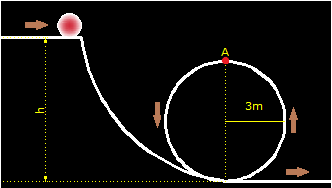
Respuesta: v = 5,42m/s, h = 7,5m

Solución

Analizamos los pasos de la bola por el punto más bajo (I) y más alto (II) del bucle vertical.

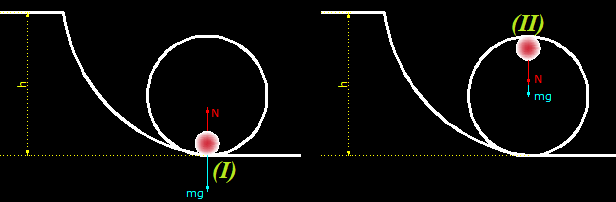
En (I) la bola está sometida a la fuerza de la gravedad y por reacción actúa el suelo del bucle (la Normal) con dirección al centro del bucle.

¿Cuánto vale la Normal en la posición (II)?

Ahora el suelo del bucle lo tiene ENCIMA, no está debajo lo que significa que no hay fuerza Normal, o si quieres, N = 0.

No olvidemos que estamos analizando un movimiento circular y que cuando la bola se halle en la posición (II) NO SE DEBE CAER sino continuar el camino que señala el bucle.

Recuerda que en todo movimiento circular existe una Fuerza centrípeta:

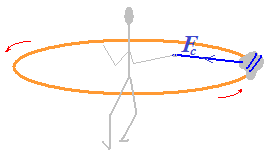
Esta Fuerza centrípeta (F_c) es la que produce el cambio de dirección de la velocidad que se produce en cada instante.

El móvil tiende a seguir su camino recto, es la cuerda la que ejerce una Fuerza y mantiene su movimiento circular.

¿Cuál es el valor de la F_c en la posición (I)?

Simplemente: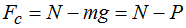  

¿Cuál es el valor de F_c en la posición (II)?

Según la figura tanto el peso P como la Normal tienen el mismo sentido:

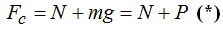
Pero no nos olvidamos que en ese punto, N vale 0.

Como hay una variación de velocidad (aunque se mantenga constante está variando su dirección) se produce una aceleración centrípeta. Lo estudiamos en el Tema correspondiente a la Cinemática: la aceleración centrípeta nos viene dada por 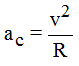 siendo v la velocidad lineal.

La Fuerza centrípeta será: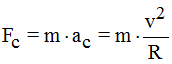  

Esta Fuerza debe ser, por lo menos, igual al peso del móvil.

Establecemos la siguiente igualdad: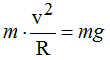 

Simplificando ambos miembros de la igualdad por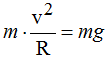  

También podíamos haber llegado al mismo resultado desde (*)  

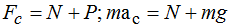 donde sustituimos la a_c por su valor:

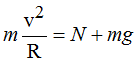 y como N en el punto A vale 0 simplificando los dos miembros de la igualdad por m llegamos a: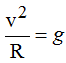 

Sustituyendo valores que conocemos: 

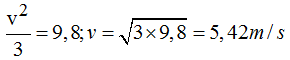
Para lograr la velocidad indispensable que acabamos de calcular es preciso conocer la altura (h) desde la que la bola debe comenzar a deslizarse.

Contamos con los datos siguientes:

Energía cinética a la altura h: …….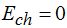 

Energía potencial en la altura h:…..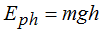 

Energía cinética en A:……………..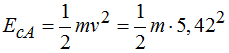 

Energía potencial en A:……………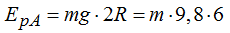  

Sabiendo que la E_mh de la bola antes de comenzar a deslizarse es: 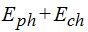  y la 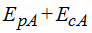 siendo ambas Energías mecánicas son iguales, establecemos la igualdad siguiente: 

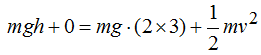
Completando sustituciones de valores conocidos y simplificando por m que lo tenemos como factor en todos los términos:

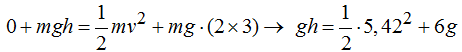
Despejamos el valor de h: