Fuerzas Conservativas y fuerzas no conservativas
Fíjate bien en los dos detalles que se te indican a continuación:
1. Estudiamos anteriormente que el Trabajo dependía de la Fuerza aplicada a un cuerpo, del espacio recorrido por éste y por el coseno del ángulo que forman la dirección de la Fuerza y el desplazamiento:
W = F . d . cosα
2.- Nos referimos ahora al último problema 2.29:
Observa que la Ep cuando desciende 30m vale (llamemos punto A):
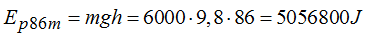
Cuando desciende 60m (llamemos punto B) es de:
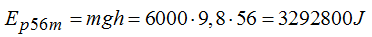
Vemos que ha pasado de 5056800J (A) a 3292800J (B).
El Trabajo que supone pasar de una altura A (inicial) a otra B (final)equivale a:
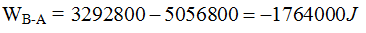
Recordando que Δ significa la diferencia o incremento del valor en B menos el valor en A:
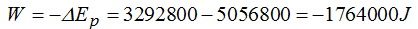
Ec a su paso por A (30m de descenso):
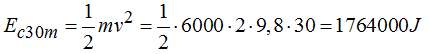
Ec a su paso por B (60m de descenso):
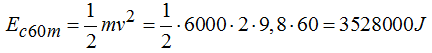
Comprobamos que:
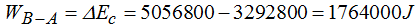
Observando detenidamente lo que tenemos más arriba podemos decir que:
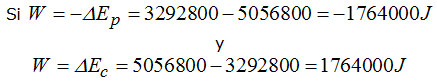
Llegamos a:
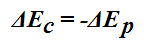
Esta igualdad equivale también a: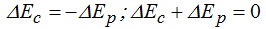 
sacando factor común al incremento nos queda:
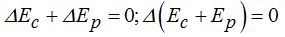
De dos factores cuyo producto es cero: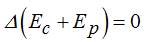 
es necesario que uno de ellos sea igual a cero y como el Δ no lo es (por tratarse de un incremento, el valor de una diferencia en este caso) quien debe ser igual a cero es el factor entre paréntesis:
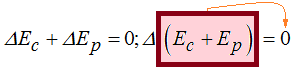
Si la Em = Ec + Ep vemos que la Energía mecánica vale cero.
Lo que hemos deducido en los puntos a 30 y 60m del descenso podíamos haberlo realizado en cualquier otro punto y hallaremos el mismo resultado: la Em se mantiene constante e igual a 0.
Hemos dicho que el Trabajo lo expresamos por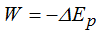 
¿No te has fijado en que para el cálculo del Trabajo no hemos tenido en cuenta la distancia recorrida?
Nos basta con conocer la Ep en dos puntos sin importarnos el camino recorrido.
En el caso que estamos estudiando hay una sola Fuerza que está actuando, se trata de la Fuerza de atracción de la Tierra.
Tratamos al contenido del problema anterior como un sistema cerrado para otras fuerzas como la de rozamiento.
Con cuanto antecede definimos a la Fuerza Conservativa (en nuestro caso la Fuerza gravitatoria - mg) a la que el Trabajo que realiza al aplicarle al cuerpo en su desplazamiento para trasladarle del punto A al punto B, NO DEPENDE del camino recorrido sino de las posiciones de ambos puntos.
Si lanzas una pelota hacia arriba:
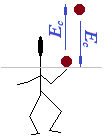
aplicas una Fuerza para que la pelota ascienda.
Debes contrarrestar la fuerza de atracción de la Tierra.
A medida que la pelota asciende, disminuye su Ec pero aumenta su Ep hasta que se para y comienza el descenso.
En el descenso irá aumentando su Ec e irá disminuyendo su Ep.
En un sistema aislado, es decir, en el que no intervengan otras fuerzas más que la de atracción de la Tierra, la velocidad de partida y de llegada al pasar por la línea horizontal gris serán iguales lo mismo que su Ec vemos que se mantiene, conserva su valor.
La Fuerza de la gravedad, esta Fuerza es conservativa.
3.30 ¿Con qué Ec llega al suelo una piedra de 2kg al dejar caer de 20m de altura? No se tiene en cuenta el rozamiento del aire.
Respuesta: 392J
Solución
La Em al comienzo (i) de la caída y al final (f) de la misma valen lo mismo, es decir: Em = Eci + Epi = Ecf + Epf
Sustituimos valores teniendo en cuenta que al comienzo de la caída no hay Ec ni Ep a la llegada:
Eci + Epi = Ecf + Epf; 0 + 2 . 9,8. 20 = Ecf + 0; Ecf = 392J
3.31 Dejamos caer una piedra de 10kg y una pelota de 100g desde 10m de altura. ¿Cuál de los dos llega al suelo con mayor velocidad teniendo en cuenta que solamente interviene la Fuerza de la gravedad (no se tiene en cuenta la Fuerza del rozamiento del aire)?
Respuesta: Ambos con 14m/s
Solución
Sabemos que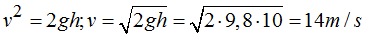 
La masa no interviene en la fórmula.
3.32 Un objeto se desliza (no se tiene en cuenta el rozamiento) por la trayectoria que une los puntos A y B de la figura siguiente:
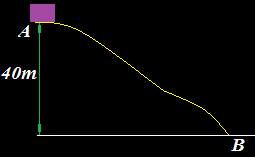
Al comprobar que la única Fuerza que actúa sobre el objeto es la de la gravedad y ésta es conservativa, podemos decir que la Ep del objeto en A tiene el mismo valor que la Ec en B por lo que:
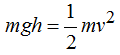
Simplificando por m y haciendo operaciones obtenemos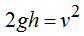 
lo que equivale, sustituyendo valores:
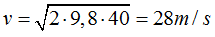
Recuerda que al tratarse de una Fuerza conservativa la Energía se conserva y no nos interesan el camino recorrido por el objeto ni su peso.
