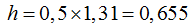La fuerza elástica de un resorte otra fuerza conservativa
La Fuerza elástica de un muelle, mientras no sobrepasemos sus límites de tolerancia (no lo deformemos), se conserva siempre que prescindamos de otras Fuerzas.
Estudiamos al tratar los resortes o muelles que la Fuerza según la ley de Hooke equivale a: F = - kx
El signo menos se debe a que siempre se opone al movimiento:
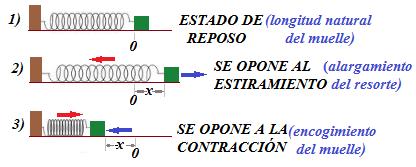
Las flechas azules representan las Fuerzas que aplicamos, las rojas las elásticas.
Sabemos que el Trabajo lo calculamos sirviéndonos de:
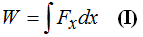
Los valores del intervalo los tendremos en cuenta en el momento de la resolución de un ejercicio o problema ajustándonos al contenido del enunciado.
Estudiamos al tratar los resortes o muelles que la Fuerza según la ley de Hooke equivale a: F = - kx
Ahora la función en x es: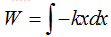 
cuyo resultado es:
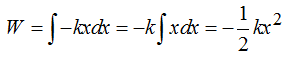
Un muelle que se esté comprimido es indudable que posee una Energía potencial que la usará para volver a su posición normal.
Su valor depende de la constante k y de x (posición del extremo del muelle).
La Energía potencial elástica es: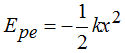 
3.37 Imagina que lanzamos una bola de acero rodando sin rozamientos cuyo peso es de 1kg hacia el tope de un resorte en posición de reposo a una velocidad de 20m/s:
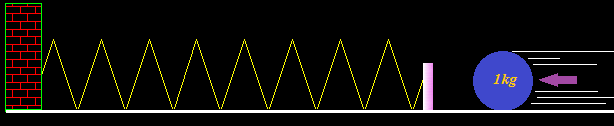
Como es natural, por efecto de la Ec de la bola se produce una compresión del muelle cuya constante k =100N/m:
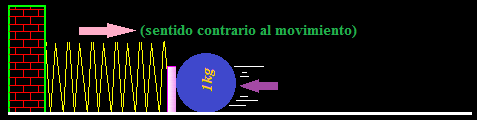
¿Cuántos centímetros se ha comprimido el muelle?
Respuesta: 2m.
Solución
Hemos de partir de que la bola llega al extremo libre del muelle con una
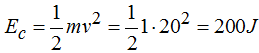
Supongamos que el muelle se contrae una distancia de – x (ponemos el signo menos para indicar el sentido del movimiento del muelle en su contracción o compresión).
Mientras ha durado la contracción del muelle se ha ido perdiendo Ec (la bola) y ganando Ep (el muelle).
Cuando el muelle ha finalizado su compresión es que ha acumulado una Ep de 200J lo que nos permite escribir, para conocer el valor del desplazamiento del muelle en sentido negativo (- x):
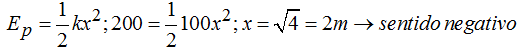
3.38 Supongamos que tenemos un muelle vertical sobre el que hemos colocado una bola de 200g y el muelle se ha comprimido 8 cm.
La constante k del muelle vale 300N/m.
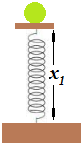
Si comprimimos el muelle 20 cm (sentido negativo):
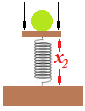
y seguidamente lo soltamos ¿hasta qué altura ascenderá la bola por efecto de la Fuerza conservativa del muelle al recuperar su posición de equilibrio?
Respuesta: 6,89m
Solución
La Ep del muelle al comprimirlo 20cm equivale a:
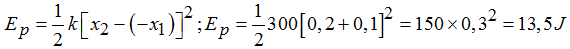
Sabemos que la por lo que:
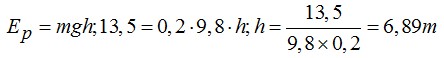
3.39 En la figura siguiente tienes un bloque del que tenemos que calcular con la velocidad con la que es despedido el bloque según
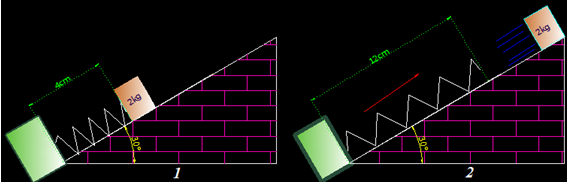
los datos que constan en la misma y sabiendo que k = 200N/m.
La Fuerza que actúa en este sistema es la conservativa elástica solamente.
Respuesta: 0,8m/s
Solución
Vemos que el muelle en su estado normal tiene 12 cm de largo.
Una vez comprimido mide 4cm. Significa que lo hemos reducido 12 – 4 = 8cm.
En el momento que el muelle queda liberado transmite al bloque la Ep que tiene almacenada y que equivale a:
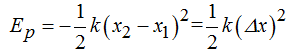
Al no haber rozamientos esta Ep se transforma en Ec del bloque: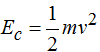 
por lo que podemos igualarlas: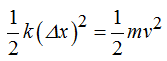 
Simplificando y sustituyendo valores que conocemos obtenemos:
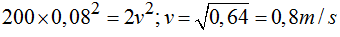
3.40 Con los datos del problema anterior calcula la aceleración con la que se ha puesto en marcha el bloque (no se tiene en cuenta el rozamiento).
Respuesta: 4,9m/s2
Solución
Dibujamos con los datos que conocemos:
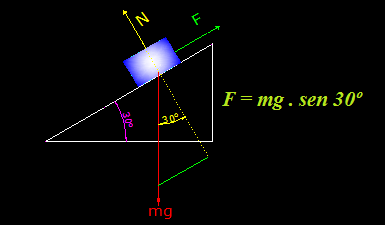
La Fuerza según observamos en la figura equivale a: mg.sen30º
Simplificando y haciendo operaciones: a = g.sen30º; a =9,8.0,5 = 4,9 m/s2
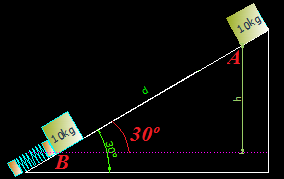
3.41 En la figura:
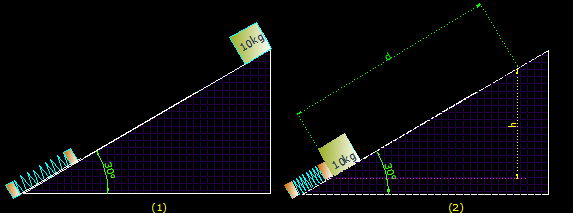
vemos en (1) un bloque de 10kg a punto de deslizarse (suponemos sin rozamiento) por un plano inclinado de 30º de inclinación. En la parte baja del mismo hay un resorte de k = 200 N/m cuya longitud, en su estado natural, es de 2m.
El bloque en su deslizamiento sobre el plano inclinado (2) comprime al muelle hasta dejarlo en una longitud de 1,2 m.
Calcula la distancia recorrida por el bloque y la altura que ha descendido.
Respuestas: d = 1,31m, h = 0,655m
Solución
La Energía mecánica en el punto A es la misma que la que hay en el punto B:
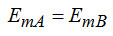
Nos permite escribir: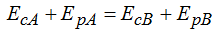 
La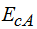 
vale 0 porque el bloque está detenido, no hay velocidad.
La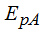 
es la Energía elástica acumulada es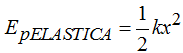 
La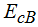 
vale 0 en el momento en el que el muelle está comprimido, no hay velocidad.
La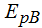 
es 0, no hay altura porque he tomado como valor de ordenada y = 0 en el punto B:
Volviendo a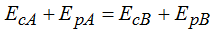 
observo que en el primer miembro de la igualdad me queda 
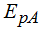y a la derecha la 
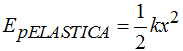(la del muelle contraído donde x = 2 – 1,2 = 0,8m).
Hemos llegado a: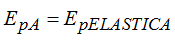 
La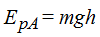 
El valor de h lo obtengo de: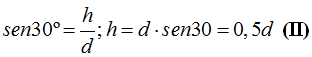 
Lo sustituyo en (I):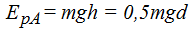 
La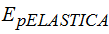 
es: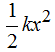 
Igualando estos dos valores y sustituyendo los valores conocidos llegamos a:
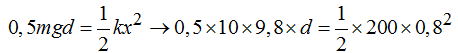
Despejamos d: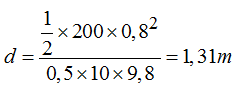 
El valor de h lo obtengo de (II): 
