Ejercicios
4.65 ¿No te han surgido dudas o inseguridades en algunas ocasiones cuando tienes que resolver problemas que tengan que ver con presiones, velocidades, secciones, etc.?
¿Cómo harías un sencillo resumen de lo estudiado sobre los fluidos en lo referente a estos aspectos de velocidades, presiones, secciones…?
Respuesta – Resumen:
- Cuando un fluido no se mueve, es decir, está en reposo, (Hidrostática) la presión en un punto de su interior depende de la altura del fluido que tiene encima y de la densidad del mismo. No soporta la misma presión un objeto situado a 2m de profundidad que a 1m y tampoco es lo mismo que el fluido sea agua que mercurio. La forma o sección del recipiente no importa, sólo la altura y la densidad del fluido que se halle en su interior.
- Cuando un recipiente descansa sobre el suelo, una mesa, etc., ejerce una presión sobre el objeto en el que descansa. Al peso-fuerza (newtons) correspondiente a una unidad de superficie de contacto, generalmente el cm2, llamamos presión (p) : p =F/S.
- La ecuación de Bernoulli se aplica a fluidos en movimiento (Hidrodinámica). El comportamiento de los fluidos en movimiento difieren un poco de los que se hallan en reposo. En este caso trabajamos con la suma de las energías de los fluidos que se mueven sabiendo que se mantiene constante a lo largo de su trayectoria. En la ecuación de Bernoulli cuando una variable aumenta su valor, otra disminuye para que se mantenga la constante.
4.66 Para que el agua de la manguera alcance el lugar que necesita, la señora de la fotografía reduce el orificio (sección) de salida de la manguera lo que produce una mayor velocidad de salida:
Suponiendo que la manguera tiene un diámetro interior de 2cm y la señora en la salida del agua lo reduce a 1cm ¿a qué velocidad sale el agua si por la manguera circulan 2litros de agua por segundo?
Respuesta: 2546,48 cm/s
Aplicamos la fórmula del caudal = Sección . velocidad y después despejamos la velocidad:
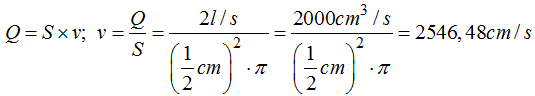
Observación: Ten en cuenta que el texto del problema nos habla de litros y de centímetros. Lo más fácil es pasar los litros de agua a gramos o cm3 para evitar equivocaciones.
4.67 La siguiente figura representa una tubería por donde fluyen 200 litros/s agua:
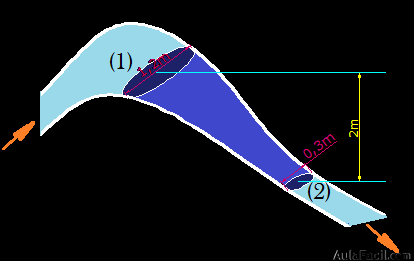
Puedes ver que la tubería es un poco irregular. Tiene una inclinación de 2m de altura entre Sección superior (1) de 1,2m de diámetro donde se registra una presión de 100 Pa y la inferior (2) de 0,3m de diámetro se desea saber la presión en este punto.
Respuesta: 115,55Pa
Solución
Para utilizar la ecuación de Bernoulli necesitamos conocer la velocidad del agua por la Sección de 1,2m de diámetro y la Sección de 0,3m de diámetro.
La cantidad de agua que pasa por ambos puntos es la misma lo que quiere decir que aplicando la ecuación de continuidad:
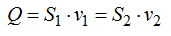
Como las cantidades de agua por unidad de tiempo por los puntos (1) y (2) es la misma nos permite hallar las velocidades.
Sustituyendo valores conocidos podemos escribir:
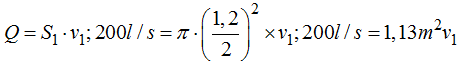
Observa que a la izquierda de la igualdad tenemos litros/s y a la derecha m2.
Tratándose de agua sabemos que 1 litro equivale a un volumen de 1dm3 pasamos los litros/s a dm3/s:
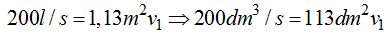
Despejamos el valor de v1 y expresamos el valor en m/s:
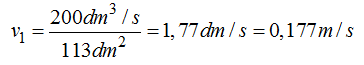
Calculamos la velocidad del agua por el punto (2):
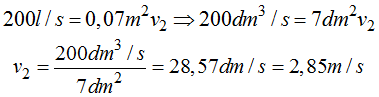
A partir de este momento podemos utilizar la ecuación de Bernoulli:
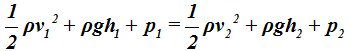
para poder calcular, sustituyendo valores que conocemos, la presión en el punto (2):
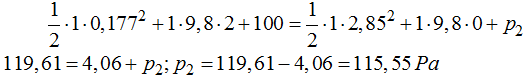
4.68 El depósito que tienes en la figura siguiente contiene un líquido de densidad 1500kg/m3.
En el interior tenemos un objeto de forma paralelepípeda con un área de la base de 5m2.
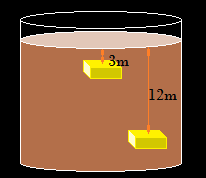
Este objeto lo introducimos a 3 y 12m de profundidad.
Calcula la diferencia de presiones a la que le hemos sometido.
Respuesta: 132300N/m2
Solución
La presión depende de la densidad del líquido y de la altura nada más.
Presión a 3m de profundidad:
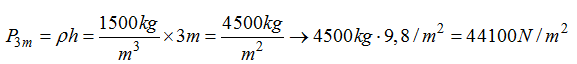
Presión a 12m de profundidad:
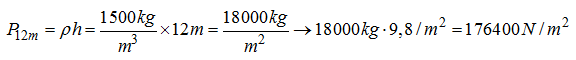
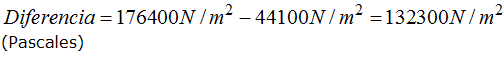
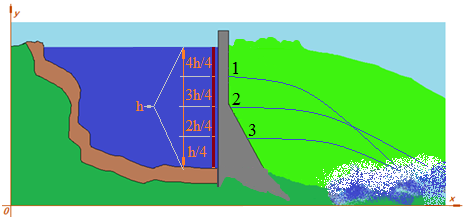
4.69 Haz un sencillo dibujo en el que veamos salir 3 finos chorros de agua a través de 3 pequeños orificios realizados a un muro de contención de un embalse.
Calcula las velocidades con las que sale el agua por cada uno de los orificios en modo de fórmula aplicable a cualquier problema que nos presenten indicándonos, en cada caso, el valor de la altura.
Respuesta: Dibujo y Cálculo de la velocidad de salida del agua
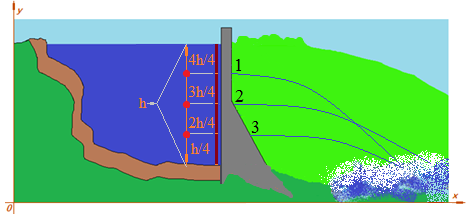
Si la altura total es h (desde el fondo hasta la superficie libre del agua del embalse) y tiene 3 divisiones (orificios) quiere decir que hemos creado 4 partes de h.
El primer orificio (1) se halla a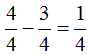 
de h bajo el nivel de agua encima tiene 1/4 de la altura total del agua).
El segundo orificio (2) está a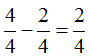 
de h bajo el nivel del agua del embalse (encima tiene 2/4 de la altura total del agua).
El tercer orificio (3) está a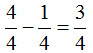 
de h bajo el nivel del agua.
(Encima tiene 3/4 de la altura total del agua).
Tenemos en cuenta el agua que se halla sobre cada uno de los orificios para calcular la velocidad inicial de salida del chorro de agua por cada uno de los orificios.
La velocidad de salida del agua por el orificio (1) es:
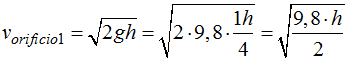
La velocidad de salida del agua por el orificio (2) es:
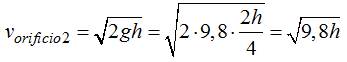
La velocidad de salida del agua por el orificio (3) es:
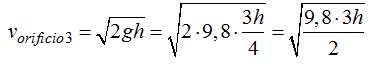
4.70 Suponiendo que la altura del agua del embalse del problema anterior es de 80m, calcula la velocidad de salida del agua por cada uno de los orificios.
Respuestas: 19,8m/s, 28m/s y 34,29m/s
Hacemos uso de las fórmulas obtenidas en el problema anterior.
Velocidad de salida del agua por el orificio superior (1):
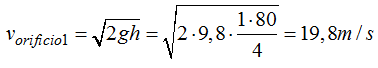
Velocidad de salida del agua por el orificio (2):
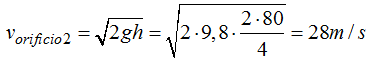
Velocidad de salida del agua por el orificio inferior (3):
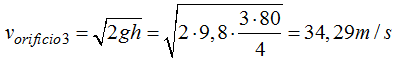
4.71 En la figura siguiente:
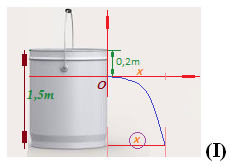
el centro del eje de coordenadas corresponde al lugar donde se halla el orificio de salida que como vemos se encuentra a 0,2m del nivel del agua teniendo en cuenta que el balde se halla lleno de agua.
¿Cuánto mide la distancia alcanzada (x, eje de abscisas) por el chorro de agua (en los primeros instantes) con relación a la base del envase de plástico sabiendo que éste mide 1,5m de altura?
Respuesta: 1m
Se trata de un movimiento parcial parabólico y sabemos, de haberlo estudiado en Cinemática, que en el movimiento parabólico existen dos componentes: horizontal (referido al eje de abscisas) y otro vertical (referido al eje de ordenadas) actuando cada una por su cuenta:
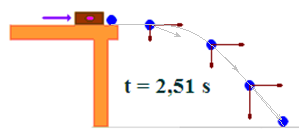
En la figura ves una bola de billar a la que le damos un golpe horizontal con una maza y sale lanzada (horizontalmente) de la mesa.
Despreciando el rozamiento del aire, la velocidad inicial vx con la que sale impulsada horizontalmente se mantiene constante hasta llegar al suelo.
Observa bien en que la velocidad referida al eje x se mantiene constante.
La componente vertical vy cada vez se hace mayor en sentido negativo debido a la aceleración de la gravedad.
La resultante de las componentes en cada punto que analizamos nos va señalando la trayectoria que la bola describe en su movimiento parabólico.
El tiempo que la bola tarda en llegar al suelo describiendo el movimiento parabólico y el que tarda dejándola caer de la mesa verticalmente son iguales:
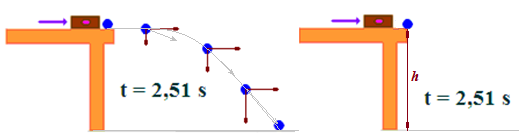
Recuerda que el problema nos pide que calculemos la distancia x o el espacio que hay entre la base del recipiente y el lugar alcanzado por la bola y para esto, necesitamos conocer el tiempo que permanece descendiendo sea con trayectoria parabólica en la que intervienen la fuerza horizontal con la que la hemos impulsado y la fuerza de la gravedad de la Tierra o la trayectoria perpendicular al suelo en la que solamente interviene ésta.
Sabemos que el espacio lo obtenemos multiplicando la velocidad por el tiempo.
Hemos llegado a deducir la fórmula que nos permite calcular la velocidad pero nos falta conocer el tiempo y para ello tomamos la fórmula del espacio aprendida en Cinemática:
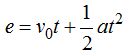
Como se trata de la caída de un cuerpo al espacio lo llamamos altura (h).
La velocidad inicial v0 al dejarla caer es 0.
La aceleración se refiere a la que ejerce la Tierra, es decir, g.
Sustituyendo valores y despejando el valor de t llegamos a:
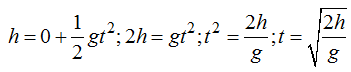
Generalizamos el problema que nos ocupa modificando un poco la figura (I):
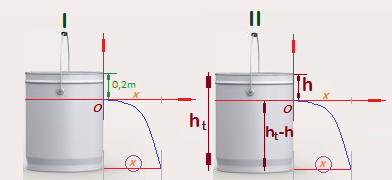
Hemos representado con ht la altura total del recipiente y con h la altura correspondiente al lugar donde se halla el orificio.
La altura desde la base del recipiente hasta el orificio es ht – h.
¿Cuánto vale ht – h?
Esta distancia corresponde al espacio recorrido en la caída de los cuerpos que anteriormente hemos deducido: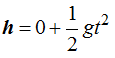
Sustituyendo valores que conocemos logramos calcular el tiempo:
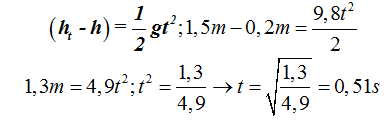
De modo general puedo escribir la fórmula del tiempo:
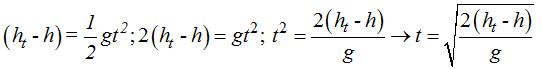
No pierdas de vista que lo que necesitamos conocer es la distancia x:
¿Con qué velocidad sale el agua del orificio?
Aplicamos:
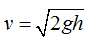
Recuerda que en esta fórmula, h representa la altura del agua que se halla sobre el orificio.
Sabemos que el espacio (x) es igual al producto de velocidad por tiempo lo que nos permite escribir:
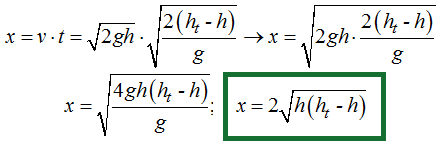
Sustituimos valores que conocemos:
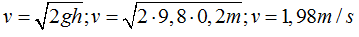
Esta velocidad (componente horizontal) se mantiene constante durante el tiempo que el agua tarda en llegar al suelo.
El espacio (x) que ha recorrido lo obtendremos al multiplicar la velocidad por el tiempo:
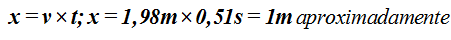
4.72 En el problema 4.69:
dedujimos el valor de las velocidades de salida del agua del embalse por cada uno de los tres orificios.
Respecto de la base del muro de contención (eje de abscisas) indica el alcance de cada uno de los chorros.
Respuestas: 69,28m, 80m y 69,28m respectivamente
Solución
En el problema 4.69 obtuvimos el modo de calcular el valor de x:
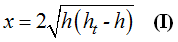
Conocemos la altura del nivel de agua del pantano: 80m.
Conocemos la altura a la que está el primer orificio:
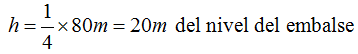
Aplicamos (I) para conocer el alcance del chorro del primer orificio:
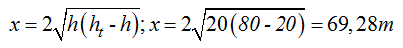
Alcance del chorro del agua que sale por el 2º orificio:
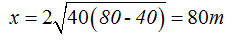
Alcance del chorro del agua que sale por el 3º orificio:
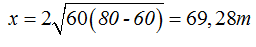
Observa: la máxima distancia alcanzada respecto al eje x es igual a la altura del nivel de agua.
Las distancias alcanzadas desde alturas iguales respecto del fondo y del nivel del agua en el embalse son iguales.
4.73 ¿Cómo calcularías el punto exacto donde haya que taladrar un muro de contención o pared de un depósito para que el chorro de agua alcance la máxima distancia conociendo la altura o nivel que alcanza?
Respuesta: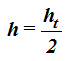 
Solución
Sabemos que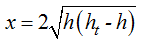 
El valor de ht es una constante a la hora de derivar. La conocemos previamente.
Vemos que el valor de x está en función del valor de h.
Si has estudiado derivadas no tenemos más que hallar la 1ª derivada igualarla a 0 y sustituir el valor que obtenemos, en la 2ª derivada y si el resultado de la sustitución es negativo en ese punto hallado hay un Máximo.
El valor de x escribimos en forma potencial por mayor comodidad a la hora de derivar:
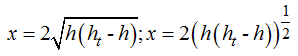
Hallamos la 1ª derivada:
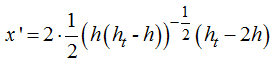
La igualamos a 0:
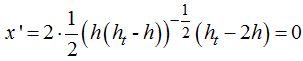
Hacemos operaciones indicadas paso a paso:
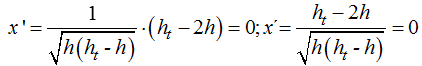
Analicemos la última expresión:
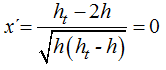
El denominador no puede ser 0 porque el cociente nos daría ∞ y nos debe dar 0. Es necesario que el numerador sea igual a 0 para cumplir con la igualdad.
En este caso,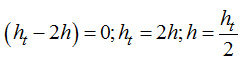 
No necesitamos calcular la 2ª derivada.
La altura a la que debemos perforar la pared se halla a la mitad de la altura del agua contenida en el depósito.
Dos datos importantes quedan calculados:
