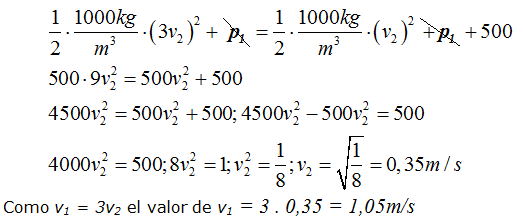Ecuación Bernoulli
Se trata de una fórmula muy importante debida a Bernoulli.
Exactamente no sabemos a qué miembro de la extensa familia Bernoulli hemos de atribuirle la ecuación.
Desde abuelo hasta nietos hubo importantes científicos en la extensa familia Bernoulli, siglo XVII-XVIII que procedentes de Holanda vivieron en Suiza.
¿A quién de ellos atribuimos la importante ecuación? No importa, todo queda en casa.
Bernoulli estableció una fórmula fundamental en el estudio de la Hidrodinámica (agua en movimiento).
Dijo, que un fluido sin viscosidad ni rozamientos ni que se le pueda comprimir y en movimiento dentro de un tubo, la suma de todas las energías se mantiene con un valor CONSTANTE en todo su recorrido.
En otras palabras, se produce el principio de la conservación de la energía (la energía ni se crea ni se destruye, se transforma).
¿A qué energías se refiere el señor Bernoulli?
Dentro del apartado de la Mecánica, hemos estudiado en Temas anteriores la Energía Cinética: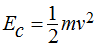
Una masa de agua a cierta velocidad posee Energía Cinética.
Sabemos que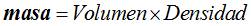
Al tratar con fluidos podemos utilizar en (I) el equivalente a la masa: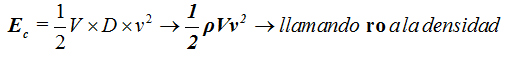
Energía Potencial: Ep = mgh
Si el tubo se halla a alturas diferentes respecto del plano horizontal, recuerda: cuanta más altura se halle una masa, mayor es su energía potencial.
Hacemos lo mismo que en la Energía Cinética, sustituimos la masa por llamando (ro) a la Densidad.
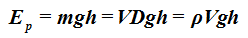
Energía - Trabajo
Cuando estudiamos el Trabajo lo asociamos con la Energía. Energía es la capacidad de hacer un Trabajo.
Si aplicamos una Fuerza a un objeto y éste se mueve decimos que realizamos un trabajo:
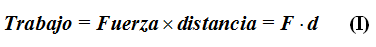
En este mismo Tema 4 estudiamos que la Presión (p) es la Fuerza por unidad de superficie:
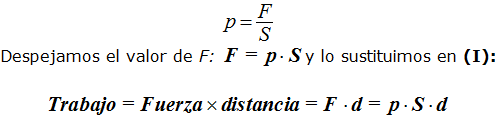
El valor de la sección (área) por el camino recorrido por segundo, en nuestro caso d, estudiamos que equivale al volumen.

Si la sección de un canal es:
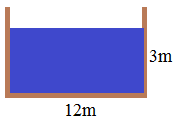
y el agua se desplaza a 5m/seg, la velocidad representa a la altura del paralelogramo:
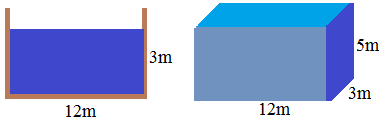
Como ves, tenemos el volumen de un prisma rectangular donde el área de la base es la sección del canal y la altura viene dada por la velocidad del fluido por segundo o la distancia recorrida en un segundo (lo estudiamos anteriormente).
Si en 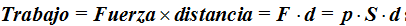 sustituimos
sustituimos 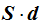 por V, llegamos a que:
por V, llegamos a que:
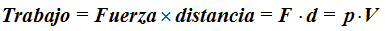
Los conceptos de Trabajo y Energía los asociamos, en la práctica significan lo mismo, se expresan en las mismas unidades (energía es la capacidad de realizar un trabajo).
Esto quiere decir que cuando una masa de un líquido se desplaza existe una energía porque se produce un trabajo.
El señor Bernoulli nos dijo algo muy importante:
 de un líquido (sin rozamientos, sin viscosidad y que no sea comprimible) en cualquier punto del tubo por donde fluye se mantiene constante.
de un líquido (sin rozamientos, sin viscosidad y que no sea comprimible) en cualquier punto del tubo por donde fluye se mantiene constante.
Lo que acabamos de estudiar significa que en la figura siguiente en los puntos donde las presiones corresponden a p1 y p2 podemos establecer la siguiente igualdad:
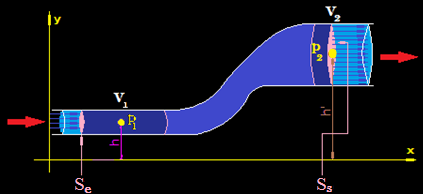
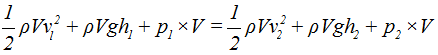
Como el volumen de líquido que pasa por unidad de tiempo es el mismo en todos los puntos que consideremos, lo simplificamos:
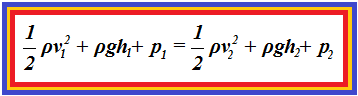
4.59 ¿Qué sucedería si el tubo, en todo su recorrido fuera paralelo al plano horizontal?
Respuesta: Al tener las alturas iguales la ecuación del recuadro quedaría simplificada:

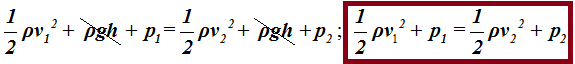
4.60 Por un tubo horizontal circula agua. El caudal es de 100litros/s.
El tubo en la parte más ancha tiene una sección de 1m2 y 0,5m2 en la más estrecha.
¿Cuál es la velocidad del agua en cada sección?
Respuestas: 100m/s y 200m/s respectivamente
Sabemos que la cantidad de agua/s nos viene dada por
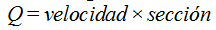
La cantidad de agua por segundo es la misma a la entrada que a la salida.
En la zona de mayor sección tenemos reemplazando valores conocidos:
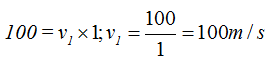
En la zona de menor sección:
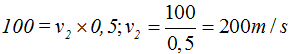
4.61 En el problema anterior indica en qué lugar la presión es mayor y porqué.
Respuesta: A la entrada la presión es mayor porque la velocidad es menor. Como es lógico, coincide con que la sección en este lugar también es mayor.
4.62 Tomando como referencia el problema 4.60 ¿cuánto vale la diferencia de presiones entre la entrada y la salida?
Respuesta: 147000000Pa
Solución
Dedujimos la ecuación de Bernoulli para tubos horizontales:
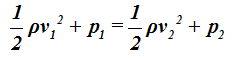
Recordamos que la densidad se refiere a la cantidad de masa o materia que un cuerpo tiene por unidad de volumen (un cm3 de un cuerpo tiene la misma cantidad de materia en cualquier parte donde se halle:
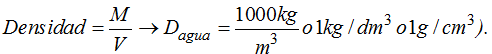
Al peso o fuerza con que la Tierra atrae a un cuerpo llamamos peso específico.
El peso específico sí puede variar porque depende del valor de g
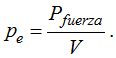
Una persona que pesa 60kg en la Tierra, en la Luna pesa 6 veces menos ya que ésta es 6 veces menor que la Tierra. Su masa sigue siendo la misma.
La densidad la podemos expresarla en kg/m3, kg/dm3 o g/cm3.
Ejemplos:
El agua tiene una densidad de 1kg/dm3 o 1000kg/m3 y un peso específico de 9,8 newtons/dm3, 9800kg/m3.
El alcohol tiene una densidad de 0,792kg/dm3 o 792kg/m3 y un peso específico (fuerza con que la Tierra le atrae ) de
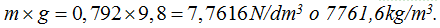
Todo lo anterior volvemos a repetirlo para evitar confusiones a la hora de utilizar la medida de la unidad que utilizamos para las presiones en este problema:
El Pascal (Pa) equivale a una Fuerza de 1 N/m2.
Sustituimos valores sabiendo que la densidad del agua es 1000kg/m3:
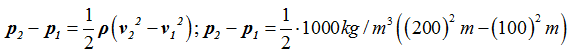
Hacemos operaciones paso a paso:
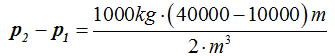
Si la presión la damos en Pascales y el pascal (p) se refiere a kilos-fuerza o newtons por m2 a la última expresión multiplicamos por g (9,8m/s2):
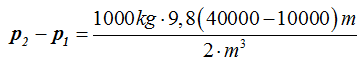
Simplificamos después de reducir términos semejantes:
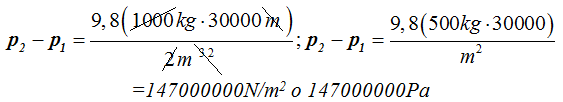
4.63 Tenemos el balde de plástico de la siguiente figura:
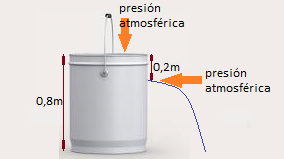
Suponemos que se halla lleno de agua, no tiene tapa.
El balde mide 0,8m de altura y a 0,2m a partir de la parte alta le hacemos un fino agujero para que salga el agua. ¿Con qué velocidad lo hace?
Ten presente, respecto de la altura del agua, la se halla encima del orificio.
Respuesta: 1,98m/s
Solución
El balde está lleno de agua. Por la parte superior, el agua está sometida a la presión atmosférica.
El agua que va a salir por el agujerito que hemos hecho, (repetimos que es muy fino, de muy poco diámetro) se va a encontrar también con la presión atmosférica.
Hacemos uso de la ecuación de Bernoulli:
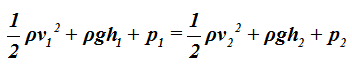
La expresión a la izquierda de la igualdad se refiere a la superficie superior abierta del balde.
La expresión de la derecha se refiere al muy fino agujero que hemos hecho al balde 0,2m de la parte superior del balde.
Vemos que en los dos lados de la igualdad aparecen las presiones p1 y p2 que por referirse, ambas, a la presión atmosférica podemos simplificarlas: 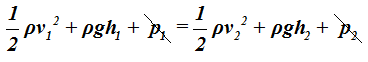
quedándonos: 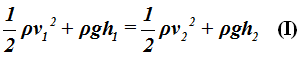
Al ser de muy poco diámetro el agujero de salida, la velocidad de salida del agua v2 es muy superior a la velocidad v1 que es la velocidad con la que desciende el nivel del agua del balde.
Este valor de v1 es tan pequeño respecto al de salida v2 que lo despreciamos.
Esto significa que el primer sumando de (I) vale 0 y esto hace que la expresión última se simplifique un poco más llegando a:
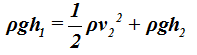
Como 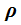 se halla en todos los términos podemos simplificar:
se halla en todos los términos podemos simplificar:
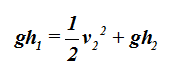
Analizamos los valores de las alturas considerándolas en un eje de coordenadas:
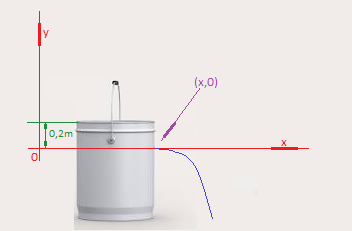
Esto significa que el valor de h2 vale 0 porque en el eje de coordenadas que hemos dibujado el valor de la ordenada es 0.
Esto hace que la última expresión obtenida la podamos reducir un poco más: 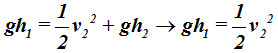
Ahora podemos despejar el valor de la velocidad de salida del agua por el pequeño orificio que hemos hecho al balde:
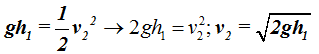
Sustituimos valores en la fórmula final obtenida:
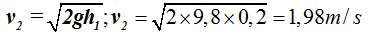
4.64 En la figura siguiente vemos un grifo manteniendo un depósito al mismo nivel:
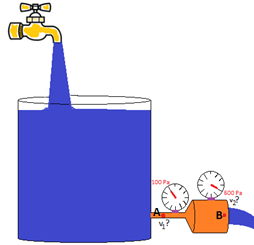
En la parte inferior tiene un orificio unido a un tubo con dos secciones distintas.
Por la sección más pequeña la presión del agua, nos indica un manómetro una presión de 100Pa, y otro en la de mayor sección 600Pa.
¿Cuáles son las velocidades del agua por las zonas más estrecha (A) (v1) cuya sección es de 5cm2 y la más ancha (B) (v2) con sección de 15cm2 del tubo de desagüe?
Respuesta: 1,05m/s y 0,35m/s respectivamente.
Solución
Sabemos que el producto de la velocidad de salida del agua por la sección en la zona estrecha del tubo de desagüe por la sección del tubo en este lugar es igual al producto de la velocidad de salida del agua por el valor de la sección en la parte más ancha:
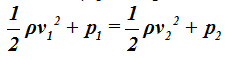
Hemos sustituido valores y simplificado por 5 a la última igualdad.
Conocemos los valores de las presiones en la zonas: estrecha (100Pa) y ancha (600Pa) lo que significa que:
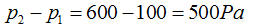
Despejamos el valor de p2:

Aplicamos la ecuación de Bernoulli:
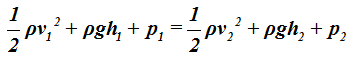
Eliminamos los sumandos que representan a la energía potencial por ser iguales. Son iguales por tener iguales las alturas (A y B se encuentran a la misma altura) y nos queda:
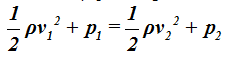
Sustituimos valores que conocemos, reducimos términos semejantes, simplificando y haciendo paso a paso las operaciones indicadas llegamos (recuerda que anteriormente calculamos el valor de p2 en función de p1 y v1 en función de v2):