¿Cómo se explica que el chorro de agua que sale del orificio inferior no alcance la máxima distancia sí sale con mayor velocidad
¿Cómo se explica que el chorro de agua que sale del orificio inferior no alcance la máxima distancia (x) si sale con mayor velocidad que los chorros que tiene encima?
Sabemos que en un movimiento de trayectoria parabólica tenemos:
El movimiento horizontal (referido al eje de abscisas) se mantiene constante.
En el movimiento vertical (referido al eje de ordenadas) se ve sometido a g con signo negativo en el ascenso y positivo en el descenso.
Ambos movimientos actúan por separado, se ignoran.
Lo que nos interesa saber, en este caso, es la altura a la que está situado el orificio respecto al suelo.
Sencillamente que cuando el agua sale del orificio inferior tiene menos tiempo en llegar al suelo porque se encuentra a menor altura y sabemos que en el valor de x interviene este factor (espacio = velocidad . tiempo).
4.74 ¿Qué se te ocurriría hacer para demostrar que efectivamente el chorro inferior sea el que más se aleje?
Respuesta: Solución
Se me ocurre colocar el depósito que contiene el agua a bastante altura como en la foto siguiente (rara construcción ya que ocupa una parte de la calle o carretera) y las medidas las pongo sin tener en cuenta las reales:

Dibujo un esquema elemental del mismo:
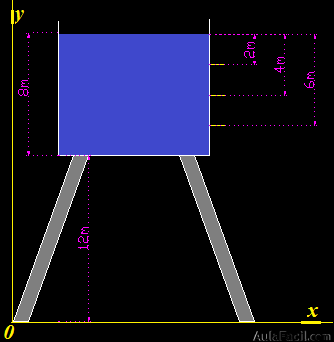
En primer lugar calculo las velocidades con que sale el agua por cada uno de los orificios teniendo en cuenta que h representa la altura de agua que está sobre el orificio respectivo:
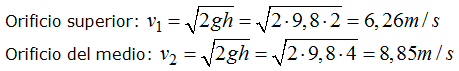
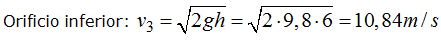
En segundo lugar calculo los tiempos que tardan en llegar al suelo sobre el que se asientan las columnas de la torre teniendo en cuenta que h representa la altura, desde el suelo hasta cada orificio, los distinguimos por el subíndice.
Tiempo que tarda en llegar al suelo el agua que sale del primer orificio:
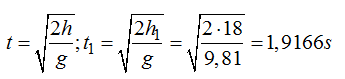
Tiempo que tarda en llegar al suelo el agua que sale del segundo orificio:
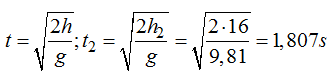
Tiempo que tarda en llegar al suelo el agua que sale del tercer orificio:
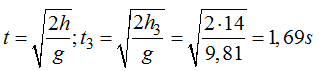
Compruebo que el tiempo menor corresponde al agua salido del orificio inferior.
Conozco la velocidad y el tiempo lo que me permite calcular los espacios o distancias (x):
Distancia entre la base de la torre y lugar de llegada del agua correspondiente al grifo superior:
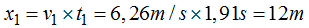
Distancia entre la base de la torre y lugar de llegada del agua correspondiente al grifo del medio:
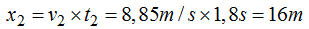
Distancia entre la base de la torre y lugar de llegada del agua correspondiente al grifo inferior:
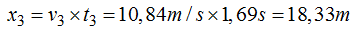
La mayor distancia alcanzada corresponde al grifo que está más abajo:

Si tenemos en cuenta como lugar de llegada del agua que sale por los orificios la base del depósito vemos que la que más se aleja es el agua que sale del orificio del medio y coinciden las distancias correspondientes al primero y tercero siempre que se hallen a la misma distancia, la superior, respecto del nivel del agua del depósito, y la inferior, respecto del fondo del mismo.

