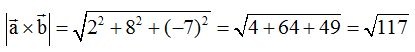Producto Vectorial de dos vectores unitarios

Si estos valores los llevas a:

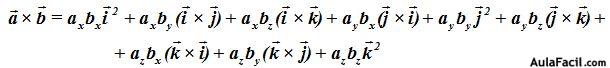
Eliminando los términos que contengan algún factor elevado al cuadrado nos quedará:

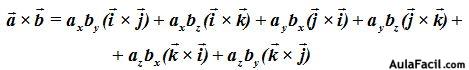
Sustituyendo el producto vectorial de los vectores entre paréntesis con sus correspondientes signos obtenemos:

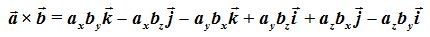
Ordenamos a los términos con el mismo eje:

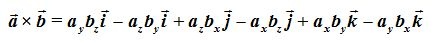
Sacamos factores comunes a :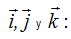

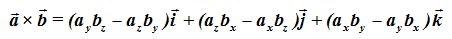
Sucede que este modo de hacer el cálculo de un producto vectorial, pocos lo utilizan.

Casi siempre se utiliza el determinante siguiente que es fácil de recordar y resolver para llegar exactamente al mismo resultado:

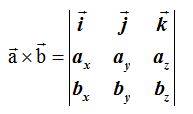
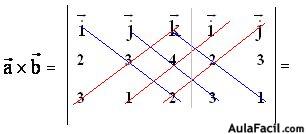
Resolvemos el determinante escribiéndolo:

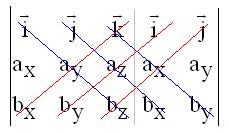
Las diagonales principales las tienes en color azul y en rojo las secundarias.

El resultado será:

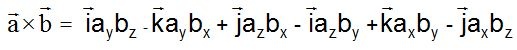
Sacando factores comunes:

Coincide con lo obtenido anteriormente:

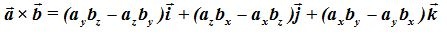
Ejemplo:

Calcula el valor del módulo del vector producto 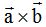, si las componentes de  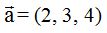 y las de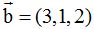 

Respuesta:

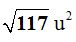
Solución

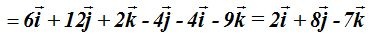
Aplicamos el teorema de Pitágoras en el espacio: