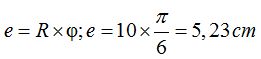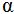Revoluciones por minuto (RPM)
Significa el número de vueltas completas que un móvil realiza por minuto.
Muchas veces conviene saber el de revoluciones por segundo.
1.83 Un móvil gira a 1500 revoluciones por minuto. ¿A cuántas r.p.s. (revoluciones por segundo) corresponden?
Respuesta: 25 r.p.s.
Solución.
Si en un minuto da 1500 vueltas, en 1 seg. dará:
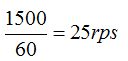
El orden que llevaremos en el estudio de esta materia será:

ELEMENTOS Y NOMENCLATURA QUE UTILIZAMOS
Ángulo girado | φ (fi) |
Espacio lineal recorrido | e |
Velocidad angular media | ωm (omega) |
Velocidad angular instantánea | ω |
Velocidad angular inicial | ωo |
Velocidad angular final | ωf |
Velocidad lineal | v |
Aceleración angular |
|
Aceleración tangencial | at |
Aceleración centrípeta | ac |
Aceleración normal | an |
Distancia desde el centro-eje de giro- al móvil | R |
Radián – ángulo cuyo arco es igual al radio | Rad |
Período – tiempo en dar una vuelta completa | T |
Frecuencia – nº de vueltas por u. de tiempo | F |
BREVE ANÁLISIS DE CADA UNO DE ESTOS ELEMENTOS
La trayectoria que describe un movimiento circular es una circunferencia por lo que podemos considerar, por un lado, el ángulo recorrido por el móvil:
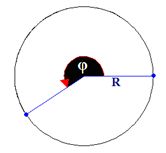
y por otro:
ESPACIO LINEAL RECORRIDO.
Se trata del camino recorrido sobre la trayectoria circular o sobre la línea de la circunferencia o el arco descrito durante el tiempo que ha durado el movimiento:
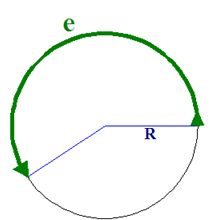
RELACIÓN ENTRE φ y e
Cuando nos referimos al radián dijimos que se trataba de un ángulo en el que la longitud del radio y la longitud del arco son iguales:
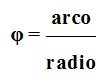
Si este cociente vale 1 podemos decir que φ vale 1 radián.
La igualdad anterior podíamos escribirla:
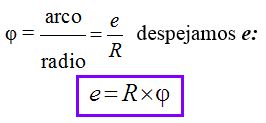
1.84 Calcula la longitud del arco correspondiente a una circunferencia de 12 cm. de radio y un ángulo φ de 60º.
Respuesta: 12,56cm
Solución.
Transformamos los 60º en radianes:
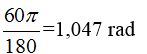
Aplicamos la fórmula: 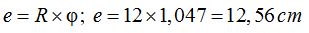
1.85 Calcula la longitud de un arco correspondiente a una circunferencia de 10 cm. de radio y un ángulo central de 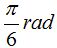 .
.
Respuesta: 5,23 cm.
Solución.
Aplicando la fórmula anterior: