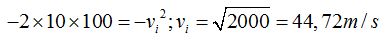Cuerpos lanzados verticalmente hacia arriba
Hasta ahora hemos estudiado la caída libre, ahora estudiaremos el móvil que se desplaza verticalmente hacia arriba.
Será preciso lanzarlo y como en el caso anterior que dejábamos caer, el móvil está sometido a la atracción de la gravedad pero ahora, la velocidad en lugar de ir creciendo segundo a segundo va decreciendo.
Si al subir verticalmente va disminuyendo su velocidad habrá un momento en que esa velocidad valdrá cero.
En ese momento habrá alcanzado la máxima altura.
Las fórmulas obtenidas anteriormente son aplicables en este caso con la diferencia de que ahora la aceleración de la gravedad actúa frenando por lo que el valor de g será negativo.
(En los problemas siguientes le das a g el valor de 10 m/s2 )
1.38 Se lanza una piedra verticalmente hacia arriba con velocidad de 60 m/s ¿qué altura alcanza?
Respuesta: 180 m
Solución.
Tomamos una fórmula que nos permite hallar la altura sin tener en cuenta el tiempo:
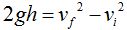
No te olvides que cuando los cuerpos ascienden, la fuerza de la gravedad actúa de forma negativa hasta lograr que su velocidad final sea cero.
Sustituyendo valores que conocemos en la fórmula teniendo en cuenta lo que acabamos de decir tendremos:
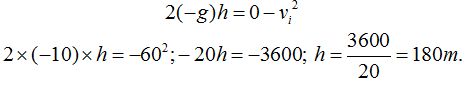
1.39 Un objeto se lanza verticalmente hacia arriba y al cabo de 8 segundos vuelve al lugar de donde partió. ¿Hasta qué altura subió si no tenemos en cuenta el rozamiento del aire?
Respuesta: 80 m.
Solución.
Si no tenemos en cuenta el rozamiento del aire tanto al subir como al bajar podemos decir que ha tardado 4 segundos en subir y 4 en bajar.
Sabemos que vf = vi - gt (cuando g es negativo).
Conocemos la velocidad final que es 0.
Calculamos la velocidad inicial: 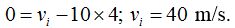
En 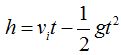 sustituimos valores y haciendo operaciones llegamos a:
sustituimos valores y haciendo operaciones llegamos a: 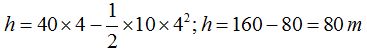
1.40 Un objeto es lanzado verticalmente hacia arriba y ha alcanzado una altura de 80 m. ¿Cuánto tiempo tardó en llegar a esa altura si partió con una velocidad de 40 m/s?
Respuesta: 4 segundos
Solución
Si observas algunos de los datos de este problema proceden del anterior que si estuviese bien resuelto, la respuesta del problema actual debe ser: 4 segundos.
Como este problema menciona el tiempo y la altura tomamos la fórmula:
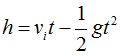
Sustituimos valores y realizamos operaciones llegando a:
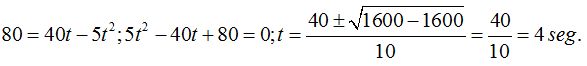
1.41 Un objeto se lanza verticalmente hacia arriba y alcanza una altura de 100 m. ¿Con qué velocidad salió?
Respuesta: 44,72 m/s
Solución.
En la fórmula a utilizar debe aparecer la altura y no el tiempo por lo que nos conviene hacer uso de:
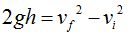
Como la velocidad final ha de ser 0 nos queda:
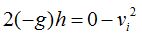
Sustituyendo obtenemos: