Transformaciones proyectivas: homología

1. Homología

Es la relación geométrica que se establece entre dos planos por medio de una proyección o radiación desde un punto exterior propio.

2. Elementos que intervienen
 

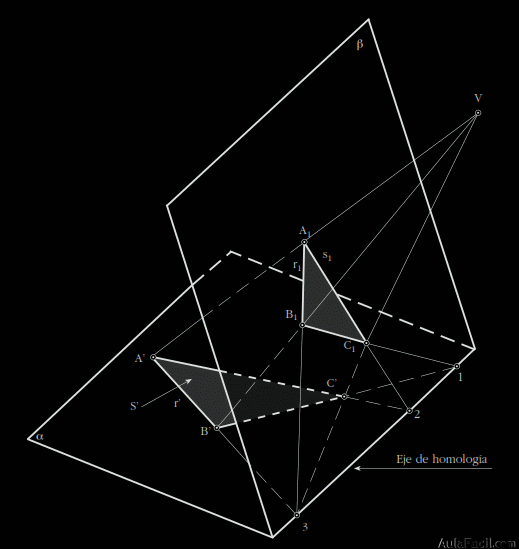
1. El centro de homología: punto V de donde parten el haz de rectas.

2. El eje de homología: recta intersección entre los dos planos.

Por otro lado, diremos que tres puntos A_1, B_1,y C₁ son homólogos
de A’ B’ C’ cuando cumplan las siguientes condiciones:

1. Estar en línea recta con el centro de homología punto V.

2. Que las rectas homólogas, por ejemplo A₁B₁ y A’ B’, se corten en puntos del eje de homología.

Esta última condición nos lleva a definir el eje de homología como el lugar geométrico de los puntos dobles, es decir, de los puntos que son homólogos de sí mismos.

2. Rectas límites

Son las rectas que definen el lugar geométrico de los puntos homólogos del infinito que corresponden a las figuras inicial y transformada.

Siendo una homología una relación entre dos figuras, existen dos rectas límite, una por cada figura.

La distancia (d) de una recta límite respecto al centro de homología es igual a la distancia de la otra recta límite respecto al eje de homología.

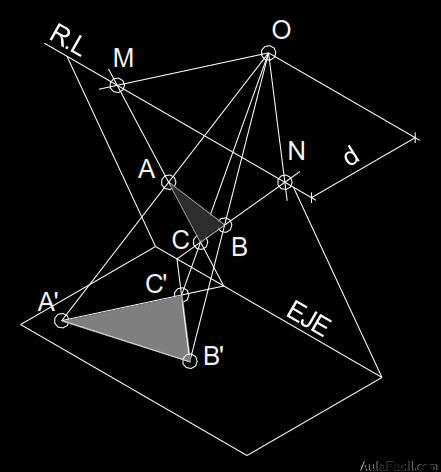
2.1 Determinación recta límite

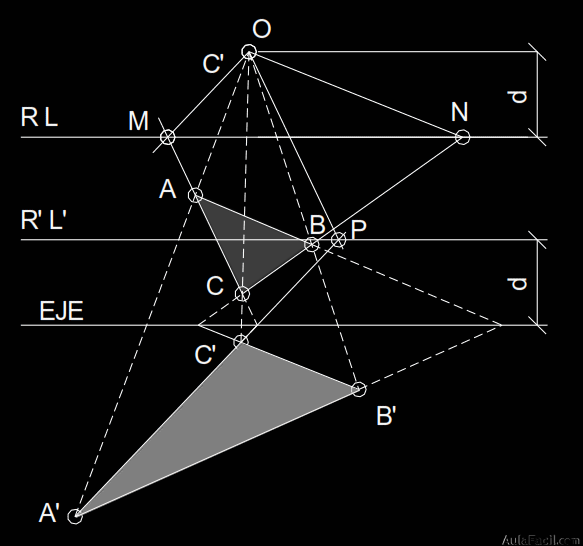
1. Por el centro de homología se traza una recta paralela a un lado homólogo (A’C’) y se prolonga el lado original (AC) hasta que corte a la paralela anterior en un punto (M).

2. Para obtener otro punto de la recta límite se sigue el mismo procedimiento: por O se traza una paralela a C’B’ y se prolonga el lado original CB hasta que ambos se corte en N.

3. Se unen los puntos hallados anteriormente (M y N) mediante una recta, que resulta paralela al eje de homología, obteniendo así la recta límite.

4. La recta límite de la figura transformada (A’B’C’) se determina siguiendo el mismo método aplicado a su homóloga (ABC).