Transformaciones proyectivas: afinidad
1. Afinidad
Dependiendo de que el centro de homología y el eje de homología sean propios o impropios, es decir, que sean conocidos o estén en el infinito, obtendremos distintos casos de homología.
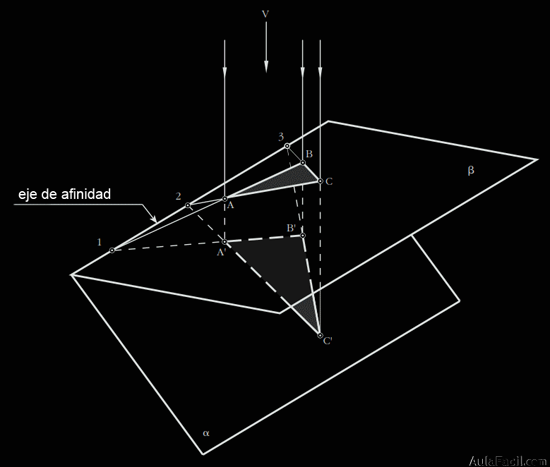
Cuando el centro de homología está en el infinito obtenemos una afinidad homológica.
La consecuencia de que el centro de homología sea impropio es que las rectas que unen puntos homólogos son paralelas.
A la dirección de éstas se le denomina dirección de afinidad (V), pudiendo ser ésta oblicua al eje de afinidad o perpendicular al mismo.
Las rectas límites serán impropias, es decir, estarán en el infinito.
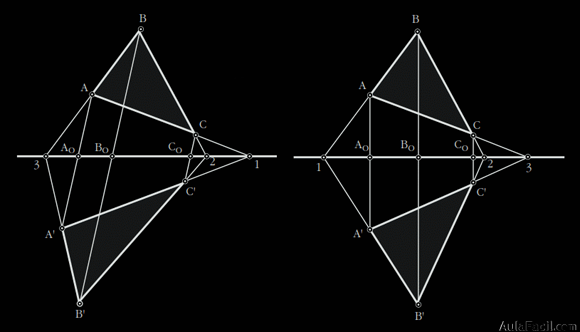
2. Razón de afinidad
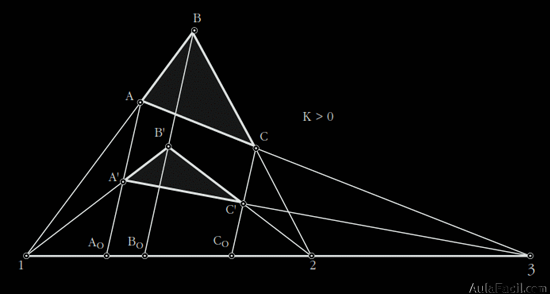
En la relación K = A0A /A0A’ = B0B / B0B’ = C0C/C0C’, a la constante K se le denomina razón de afinidad.
Si las figuras afines están una a cada lado del eje de afinidad, la razón de afinidad será negativa, K < 0.
Si las dos figuras están al mismo lado del eje de afinidad la razón de afinidad será positiva, K>0.