La elipse: definición y propiedades
1. La elipse
La elipse es el lugar geométrico de los puntos del plano cuya suma de radio vectores (distancias desde la elipse a los dos focos) es constante e igual al eje mayor.
Las tres magnitudes que caracterizan la elipse son:
1. Eje mayor AB: llamado real o principal. Es eje de simetría.
2. Eje menor CD: llamado imaginario o secundario. También es eje de simetría.
3. Focos F, F’: puntos fijos sobre el eje mayor de referencia de distancias.
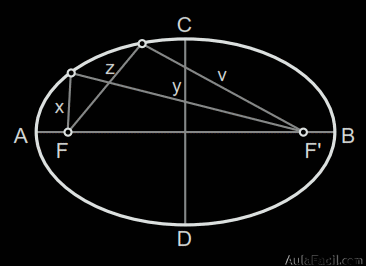
x+y=AB ; z+v=AB
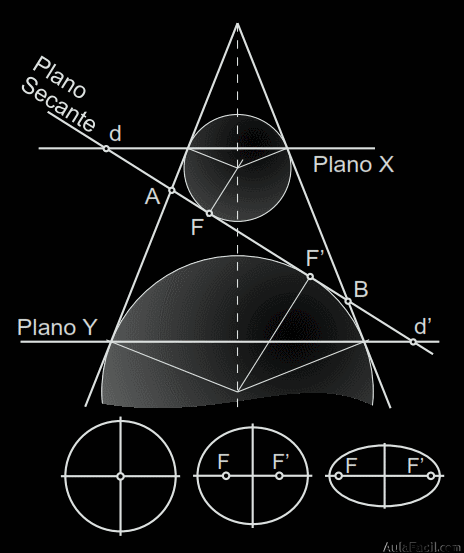
2. Elementos que intervienen (teorema de Dandelin)
1. Plano secante a todas las generatrices del cono.
2. Elipse: curva plana y cerrada que el plano secante produce al cortar las generatrices del cono.
3. Esferas tangentes al cono de revolución y al plano secante.
4. Focos, puntos F y F’ de tangencia de las esferas con el plano secante.
5. Radios vectores de la curva, PF y PF’. Pertenecen al plano secante y son tangentes a una esfera desde P. Son dos segmentos que parten de los focos a un mismo punto de la elipse.
6. Planos X e Y: planos que pasan por los puntos de tangencia de cada esfera con el cono.
7. Directrices: rectas (d,d'), intersección de los planos X, Y con el plano secante.
8. Excentricidad: es la razón constante para todos los puntos de la elipse de distancias de un punto de una cónica a un foco y a su directriz. “Es el achatamiento de la elipse” y viene marcada por el distanciamiento entre sus dos focos. Cuanto más alejados estén los focos entre sí más excéntrica será la elipse.