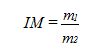Problemas de Localización

De entre los modelos deductivos de localización, nosotros examinaremos los modelos mecánicos. Son modelos que basan la determinación de la localización óptima de la unidad productiva en la consideración de un único factor, el coste de transporte, debido a lo cual, el volumen de los diferentes elementos a transportar, actúa como fuerza determinante de la localización, atrayéndola hacia los puntos donde se sitúen los factores más pesados, es decir, económicamente más costosos de transportar. Siguen la hipótesis de homogeneidad espacial que supone un espacio uniformemente dotado de una serie de condiciones económicas.

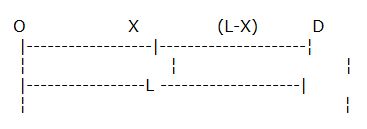
En su formulación más simple, se trata de una empresa que elabora un solo producto, que es ofertado en un mercado situado en un punto del espacio D, a partir de un solo factor significativo que obtiene de un lugar O, separado de D por una distancia L.

Bajo los supuestos planteados, es evidente que la localización óptima de la factoría se encontrará sobre algún punto del segmento OD, ya que la línea recta que une ambos puntos, O y D, representa la mínima distancia entre ambos.

Los datos del problema son los siguientes:

• L: Distancia, en kilómetros o millas, entre O y D.
• m1: Cantidad necesaria del input en unidades físicas.
• m2: Cantidad de output obtenida de las m1 unidades de input.
• t1: Tarifa unitaria de transporte del input, expresada en ptas/unidad física/kilómetro.
• t2: Tarifa unitaria de transporte del output, expresada en ptas/unidad física/kilómetro.
• X: Situación óptima de la unidad productiva, expresada en kilómetros desde el mercado de origen.

A partir de estos datos, es posible formular los costes de transporte del input (C1), del output (C2) y el coste total (C):

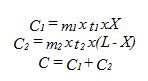
Al tratarse de funciones lineales, la solución al modelo se obtiene calculando el valor de C para los valores extremos de X, o sea, X = 0 y X = L, de manera que la localización óptima se encontrará en aquel punto en que C sea más bajo.

Cabe obtener los siguientes posibles resultados:

• Localización óptima en O: el mínimo de C corresponde a X = 0 (C1 = 0 y C = C2)
• Localización óptima en D: El mínimo de C corresponde a X = L (C2 = 0 y C = C1)
• Localización indiferente a lo largo del segmento OD: no existe un valor mínimo de C, al tomar éste el mismo valor tanto para X = 0 que para X = L

Un procedimiento simplificado para llegar al mismo resultado anterior es el que se sigue de la comparación de las pendientes de las rectas de coste de la materia prima (C1) y del producto (C2). En consecuencia, pueden plantearse los siguientes casos:

- Localización óptima en O
m1 x t1 > m2 x t2 (C1 > C2 : por kilómetro recorrido)
- Localización óptima en D
m1 x t1 < m2 x t2 (C1 < C2 : por kilómetro recorrido)
- Localización indiferente a lo largo del segmento OD
m1 x t1 = m2 x t2 (C1 = C2 : por kilómetro recorrido)

Si además se da que t1 = t2, la decisión de localización depende sólo de las cantidades a transportar de ambos, por lo que el análisis se efectúa en términos de m, a través del llamado índice material de Weber: