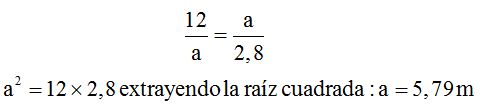Teorema del Cateto Ejercicios #52 y 53
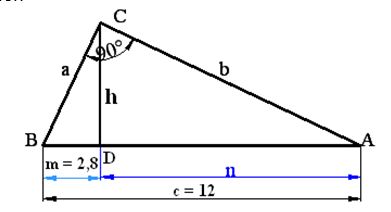
Tomamos el triángulo anterior:
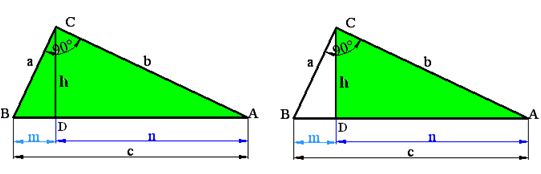
Fíjate bien en los dos triángulos en color verde. Son semejantes por lo que sus lados son proporcionales:
La hipotenusa del mayor (c) es a la hipotenusa del menor (b) como el cateto mayor del triángulo grande (b) es al cateto mayor del triángulo menor (n).
Cuanto acabas de leer lo escribimos en forma de proporción:

Lo mismo podemos hacer con:
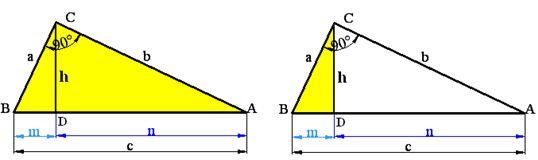
Los dos triángulos rectángulos de color amarillo son semejantes luego sus lados serán proporcionales.
La hipotenusa del mayor (c) es a la hipotenusa del menor (a) como el cateto menor del triángulo grande (a) es al cateto menor del triángulo pequeño (m).
Escribimos la proporción:
En todo triángulo rectángulo un cateto es la media proporcional entre la hipotenusa y su proyección sobre la hipotenusa.
Ejercicio #52
¿Cuánto vale la altura de un triángulo rectángulo sabiendo que las proyecciones de los catetos sobre la hipotenusa valen 5 y 9 m.?
Respuesta: 6,70 m.
Solución
Conocemos m y n
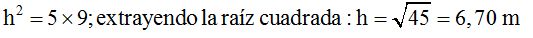
Ejercicio #53
Sabiendo que la hipotenusa de un triángulo rectángulo mide 12 m. y la proyección de un cateto sobre ella 5,6 m.¿Cuánto vale el cateto?
Respuesta: 5,79 m.
Solución