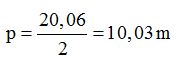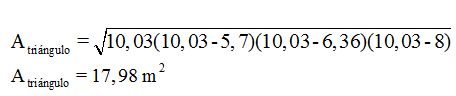Área del Triángulo-2
El perímetro de un triángulo lo obtenemos sumando las medidas de los 3 lados.
Llamamos semiperímetro a p.
En este caso: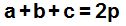 
porque 2p es el perímetro.
Llegamos a que:
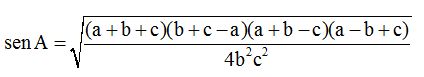
Podemos escribir del modo siguiente:
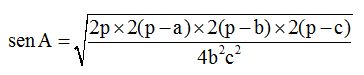
Multiplicamos en el numerador cuanto podamos:
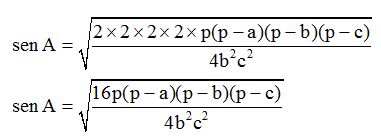
Sacamos fuera de la raíz cuadrada cuanto podamos:
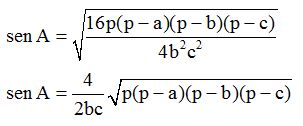
Simplificamos:
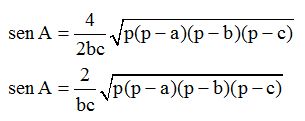
Pasamos el 2 a la izquierda de la igualdad y lo hará dividiendo. Los factores bc que están dividiendo, pasarán a la izquierda del signo =, multiplicando:
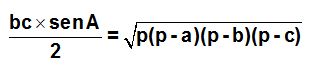
La expresión que tienes a la izquierda del signo igual es el área de un triángulo conocidos dos lados y el ángulo que forman estos dos lados, por lo tanto, la fórmula final podemos escribirla:
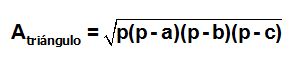
Ejercicio #59
Vamos a calcular el área del triángulo siguiente haciendo uso del seno del ángulo que forman los lados b y c, y después haciendo uso de la fórmula de Herón.
Los datos los tienes en la figura siguiente:
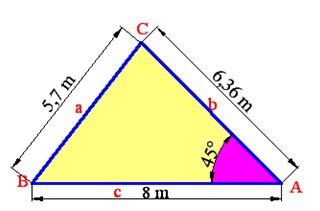
Respuesta: 17,98 m2
Solución
1ª.- Hacemos uso del sen de 45º:
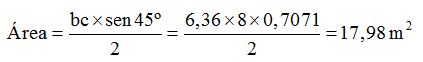
2ª.- Utilizamos la fórmula de Herón:
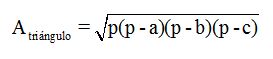
La suma de los lados es: 5,7 + 6,36 + 8 = 20,06 m.
El semiperímetro valdrá la mitad: 
