Una aplicación importante de los números

Disponemos los números combinatorios del modo siguiente:

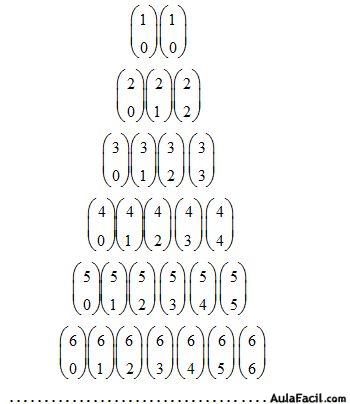
En la primera fila el número de elementos de cada número combinatorio vale 1, el número de elementos por grupo 0.
En la segunda fila el número de elementos de los números combinatorios 1, el número de elementos por grupo son correlativos partiendo de cero.
En la tercera fila el número de elementos de los números combinatorios 3, el número de elementos por grupo son correlativos partiendo de cero.
De este modo vamos construyendo el triángulo.

Teniendo en cuenta lo estudiado hasta ahora podemos escribir este triángulo como lo hicimos en el Tema 13, descrito por Tartaglia (hay quien lo atribuye a otros matemáticos):

Una aplicación importante es lo útil que resulta para cuando tenemos que elevar un binomio a una potencia:
Ejemplo:

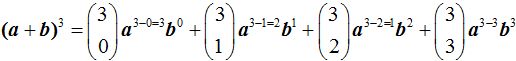
Como está elevado al cubo tomamos la tercera fila.
El primer término del binomio, en este caso a lo elevamos a la diferencia entre los dos términos de su correspondiente término complementario y el segundo término del binomio, en nuestro caso b lo elevamos al número de elementos por grupo.
Como sabemos que un número elevado a 0 vale 1 y el exponente 1 y coeficiente con el mismo valor  no los ponemos, el desarrollo anterior podemos escribir:

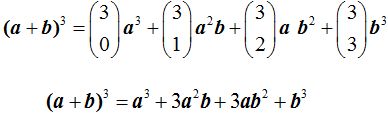
Observa que la suma de los exponentes de cada término es igual a la potencia a la que está elevado el binomio. En el ejemplo los exponentes de a y b en cada término suman 3.

18.29    En 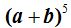¿podrías escribir el cuarto término?

Respuesta: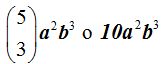 

Solución
Como los números combinatorios comienzan por cero para el número de elementos por grupo, el tercer término llevará un 2, y al término n le corresponderá  n – 1.

El coeficiente será ó 10.
El primer término del binomio llevará por exponente la diferencia entre los valores de m  y n mientras que el segundo término llevará el valor n. 

18.30    En 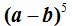 ¿podrías escribir el cuarto término?

Respuesta: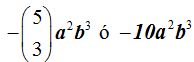 

Solución
Al tener signo + el primer término, el segundo tendrá menos, y así, se van alternando, de modo que los términos que ocupan lugar impar son positivos y son negativos los que ocupen un lugar par.

18.31  ¿Cuánto vale el término que ocupa el lugar 23 en el desarrollo del binomio ?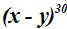

Respuesta: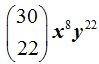 

Autor: Agradecemos a Don Ignacio Pujana el envío de este magnífico curso.