Números Combinatorios
Otro modo de representar las 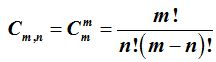 es
es 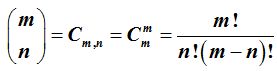
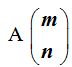 le podemos considerar como a las combinaciones que podemos hacer como m elementos tomados de n en n.
le podemos considerar como a las combinaciones que podemos hacer como m elementos tomados de n en n.
El número combinatorio 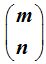 leemos: “ m sobre n”
leemos: “ m sobre n”
Ejemplo de aplicación:
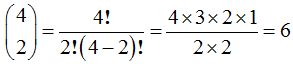
Propiedades de los números combinatorios:
1) Cualquier número entero positivo sobre cero es igual a 1
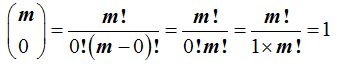
2) Cualquier número entero positivo m sobre 1 es igual a m
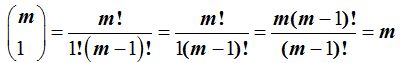
3) Cuando la suma de los números que representan el número de elementos por grupo es igual al número de elementos, podemos decir que los dos números combinatorios son iguales:
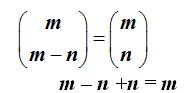
Lo comprobamos:
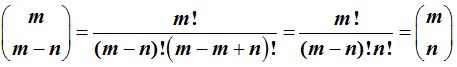
4) La suma de dos números combinatorios con el mismo número de elementos y los números que representan los elementos por grupo son consecutivos es otro número combinatorio en el que el número de elementos aumenta en una unidad y el número de elementos por grupo es el del mayor:
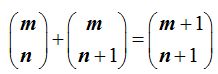
Lo comprobamos:
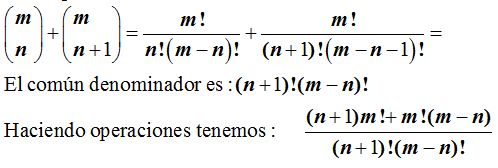
Sacamos factor común, en el numerador a, m!:
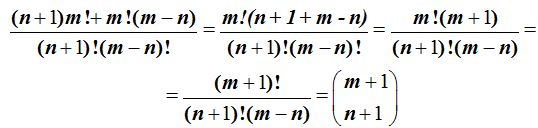
18.25 Los números combinatorios 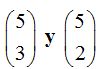 ¿son iguales?. Razona.
¿son iguales?. Razona.
Respuesta: Sí, son iguales porque la suma de los elementos de los dos números combinatorios por grupo, es igual al número de elementos.
18.26 Los números combinatorios 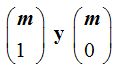 ¿son iguales?.
¿son iguales?.
Respuesta: No, el 1º es igual a m y el 2º es igual 1.
18.27 ¿Cuánto vale la suma de los números combinatorios 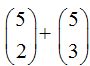 ?
?
Respuesta: 20 ó 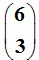
18.28 ¿Son iguales 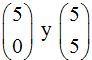 ?
?
Respuesta: Sí.

