Permutaciones con Repetición
Partiendo de un número m de elementos, llamamos permutaciones a los distintos grupos que podemos formar con los m elementos entrando todos los elementos en cada grupo.
Un grupo de otro se diferencia en el orden de colocación de sus elementos.
Tiene cierto parecido con las variaciones, su diferencia es que m y n son iguales.
Según lo que acabas de leer podemos escribir:
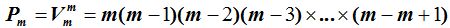
Vemos que las permutaciones de m elementos es igual al producto de m factores decrecientes a partir de m de unidad en unidad hasta llegar a 1.
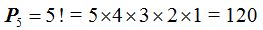
Con las 5 primeras cifras podemos hacer 120 números distintos:
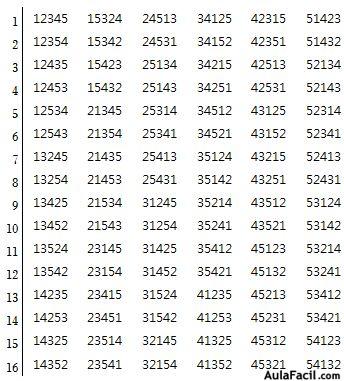

Tenemos 6 columnas de 20 permutaciones cada una, es decir, 20x6 =120 permutaciones.
Nos interesa saber el número de permutaciones y no la composición de cada grupo, lo que es complicado y tedioso.
18.7 Con las cinco primeras letras del abecedario ¿cuántas permutaciones puedo hacer?
Respuesta: 120
Solución
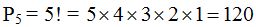
18.8 En una mesa rectangular ¿de cuántas formas diferentes pueden sentarse 12 personas a comer?
Respuesta: 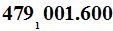
PERMUTACIONES CON REPETICIÓN 
En el caso de las permutaciones sin repetición calculábamos el factorial del número de elementos.
Cuando hablamos de permutaciones con repetición nos referimos a que hay un elemento o más de uno que se repiten.
Observa las permutaciones que podemos hacer con las letras de la palabra sal:
sal, sla, asl, als, lsa, las
Es decir, 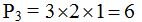
Como ves, no se repite ningún elemento en la palabra sal.
En el caso de repetir algún elemento, dos veces, como en el caso de la palabra ala, en la que el elemento a se repite dos veces, escribiríamos: 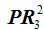
Para saber las permutaciones que podemos hacer cuando un elemento, como en el caso de la palabra ala se repite dos veces, tenemos que dividir el total de las permutaciones de los n elementos entre las permutaciones del número del elemento que se repite.
En este caso, como el elemento a se repite 2 veces tendremos:
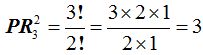
Los grupos que podemos formar son: ala, aal, laa
Las permutaciones que podemos hacer con la palabra mesa son:
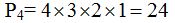
mesa, meas, msea, msae, maes, mase, emsa, emas, esma, esam,
eams, easm, smea, smae, sema, seam, same, saem, ames, amse
ames, aesm, asme, asem
Las permutaciones que podemos hacer con la palabra masa serán:
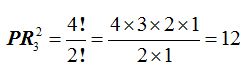
masa, maas, msaa, amsa, amas, asma, asam, aams, aasm, smaa
sama, saam
Las permutaciones que podemos hacer con la palabra banana teniendo en cuenta que el elemento a se repite 3 veces y el elemento n dos veces tendríamos 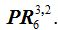
En este caso, a factorial de 6 le tenemos que dividir por factorial de 3 y factorial de 2:
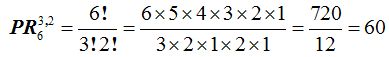
banana, banaan, bannaa, baanna, baanan, baaann, bnaana, bnaaan, bnanaa, bnnaaa
banana, abnaan, abnnaa, abanna, abanan, abaann, anbana, anbaan, anbnaa, anabna
anaban, ananba, ananab, anaabn, anaanb, annbaa, annaba, annaab, aabnna, aabnan
aabann, aanbna, aanban, aannba, aannab, aanabn, aananb, aaabnn, aaanbn, aaannb
nbaana, nbaaan, nbanaa, nbnaaa, nabana, nabaan, nabnaa, naabna, naaban, naanba
naanab, naaabn, naaanb, nanbaa, nanaba, nanaab, nnbaaa, nnabaa, nnaaba, nnaaab
18.9 ¿Cuántas permutaciones puedo obtener con la palabra paloma?
Respuesta: 360
18.10 Calcula el número de permutaciones que puedes hacer con las cifras que componen el número 113335.
Respuesta: 60

