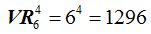Fórmula General de las V n/m
Para saber el valor de 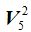 multiplicamos 5x4, es decir, dos factores decrecientes de unidad en unidad, que, generalizando podemos escribir:
multiplicamos 5x4, es decir, dos factores decrecientes de unidad en unidad, que, generalizando podemos escribir: 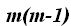
Para saber el valor de 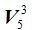 multiplicamos 5x4x3, es decir, tres factores decrecientes de unidad en unidad, que, generalizando podemos escribir:
multiplicamos 5x4x3, es decir, tres factores decrecientes de unidad en unidad, que, generalizando podemos escribir: 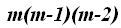
Para saber el valor de 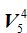 multiplicamos 5x4x3x2, es decir, cuatro factores decrecientes de unidad en unidad, que, generalizando podemos escribir:
multiplicamos 5x4x3x2, es decir, cuatro factores decrecientes de unidad en unidad, que, generalizando podemos escribir: 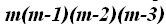
En estos tres ejemplos puedes ver que el número de elementos (m) es el primer factor, cada uno de los que le siguen van decreciendo de unidad en unidad. En último factor observamos que el valor que se le resta a m equivale al valor de n menos 1.
¿Cuál es el último factor de 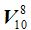 ?
?
Representando con puntos los valores de los factores intermedios será:
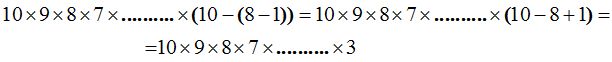
Comprobamos:
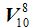 será igual a 8 factores decrecientes de unidad en unidad a partir de 10:
será igual a 8 factores decrecientes de unidad en unidad a partir de 10:
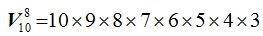
Como ves, 8 factores decrecientes de unidad en unidad a partir de 10.
La fórmula de 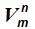 será:
será:
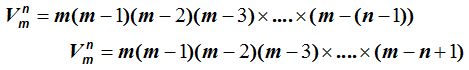
18.4 ¿Cuántas formas diferentes pueden ocupar una fila de 10 sillones 5 personas?
Respuesta: 5040 posiciones
18.5 ¿Cuántos partidos de fútbol de la primera división del fútbol del español se juegan en una temporada?. Por si no lo sabes, por ahora, la primera división la componen 20 equipos.
Respuesta: 380 partidos
VARIACIONES CON REPETICIÓN (VR) 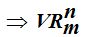
Se trata de variaciones de m elementos de orden n en las que los grupos se diferencian uno de otro, en tener un elemento distinto o en el orden de colocación pero que podamos repetir los elementos, por ejemplo:
aab aba baa
son grupos diferentes porque se diferencian en el orden de colocación de sus elementos.
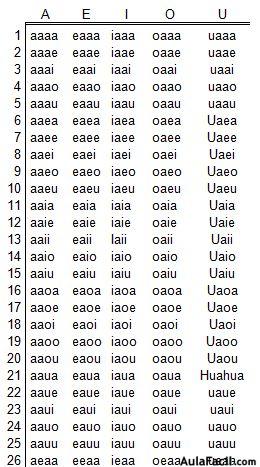
Si tomamos las cinco vocales de dos en dos veamos cuantas variaciones con repetición podemos hacer:
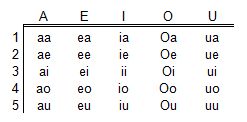
Si tenemos unos cartones, cada uno con una vocal, podemos extraer dos veces la misma vocal.
Cada grupo ves que se diferencia en tener un elemento distinto o en el orden de colocación.
Por cada vocal conseguimos 5 grupos de 2 vocales cada grupo. En total la 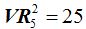 Los grupos que podemos obtener en el caso de
Los grupos que podemos obtener en el caso de 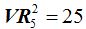
Los grupos que podemos obtener en el caso de 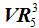 son los siguientes:
son los siguientes:
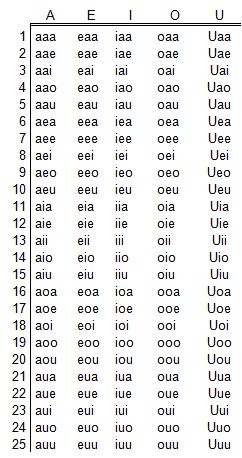
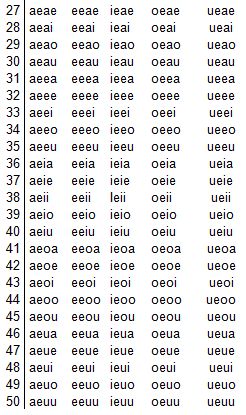
El escribir todos los grupos es una tarea un poco más complicada que en el caso anterior.
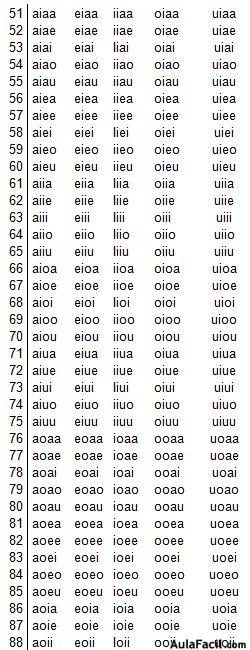
Por cada letra hemos conseguido 25 variaciones, luego el total de grupos de 3 elementos es 25x5= 125:
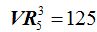
Observa si las 5 vocales las agrupamos de 4 en 4:
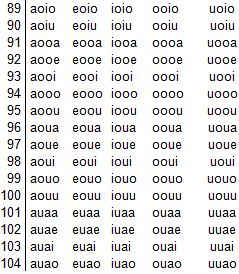
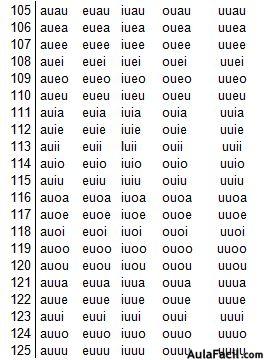
El total de grupos vemos que son 125x5= 625 variaciones con repetición:
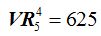
En los problemas, casi siempre, te van a preguntar el número de variaciones no cuales son.
La resolución es muy simple. Fíjate bien:
Hemos calculado que:
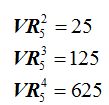
Si observas un poco te darás cuenta que si elevas el número de elementos al orden, es decir, al número de los elementos por grupo obtenemos el resultado:
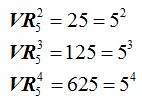
18.6 ¿Cuál es el número de variaciones con repetición que puedo conseguir con las 6 primeras cifras tomadas de 4 en 4?
Respuesta: 1296
Solución