Introducción: Plano en el Espacio
Es costumbre nombrar a los planos con las letras del abecedario griego. Por abreviar, no siempre lo haremos.
Para poder determinar, resolver o fijar un plano en un espacio tridimensional son necesarios conocer:
a) Un punto P y dos vectores 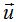 y
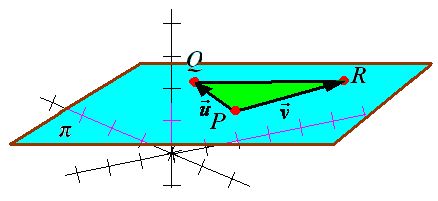
y 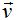 linealmente independientes como puedes ver en la figura siguiente:
linealmente independientes como puedes ver en la figura siguiente:
b) 3 puntos no situados en línea recta.
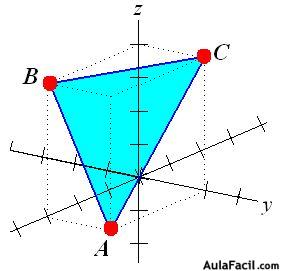
En la figura tienes tres puntos A, B, C no situados en línea recta en un eje tridimensional determinan un plano (color azul).
Recuerda que muchos aparatos de precisión descansan sobre tres patas (trípode). Tres patas, tres puntos no situados en línea recta determinan un plano.
En la resolución de problemas casi siempre utilizamos un punto y dos vectores contenidos en el plano.
Si conocemos tres puntos pero no los vectores, lo que tenemos que hacer es calcularlos.
Imagina que conocemos los puntos del plano:
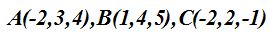
¿cuáles serían los vectores 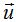 y
y 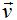 ?
?
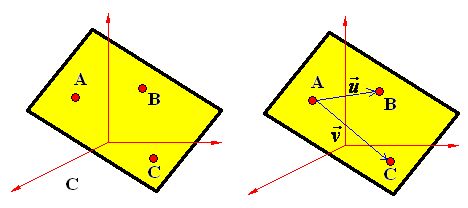
Calculamos el origen del vector 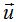 y para ello hacemos el cálculo siguiente:
y para ello hacemos el cálculo siguiente:
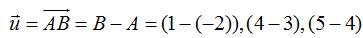
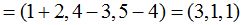
Calculamos el origen del vector 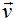 y para ello hacemos el cálculo siguiente:
y para ello hacemos el cálculo siguiente:
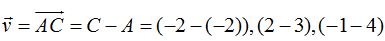
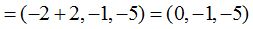
Las componentes de los vectores 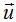 y
y 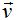 son
son 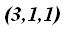 y
y 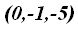 respectivamente.
respectivamente.

