Racionalizar denominadores compuestos de trinomios. Hallar la raíz cuadrada de un Polinomio.
Ejemplo:
Racionalizar:
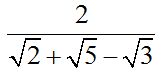 Respuesta:
Respuesta: 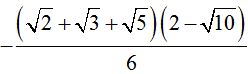
1º Juntamos dos raíces del denominador. Tomamos las dos primeras en un paréntesis: 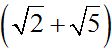 y a continuación escribimos el término que nos queda con su signo:
y a continuación escribimos el término que nos queda con su signo: 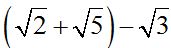 . En realidad es lo mismo que:
. En realidad es lo mismo que: 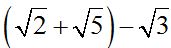 pero nos facilita para saber cual es el conjugado del denominador:
pero nos facilita para saber cual es el conjugado del denominador: 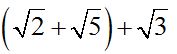 .
.
Cuidado ahora que el primer término está compuesto de dos sumandos –los que se encuentran entre paréntesis –.
2º Multiplicamos al numerador y denominador por el conjugado del denominador. Cuidado con los paréntesis:
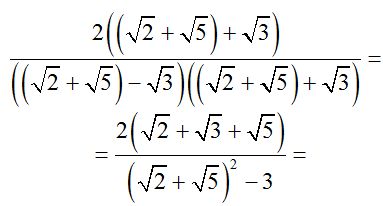
Tenemos que tener en cuenta que el primer término del denominador está compuesto de dos sumandos y al multiplicar la suma de dos números por su diferencia obtenemos la diferencia de sus cuadrados por eso el cuadrado del primer término lo escribimos como una suma indicada elevada al cuadrado: 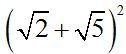 .
.
Desarrollamos el cuadrado del primer término del denominador:
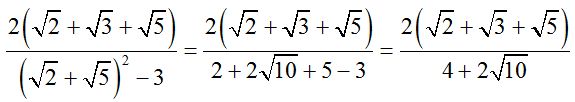
3º Tenemos que volver a multiplicar a los dos miembros de la fracción por el conjugado del denominador:
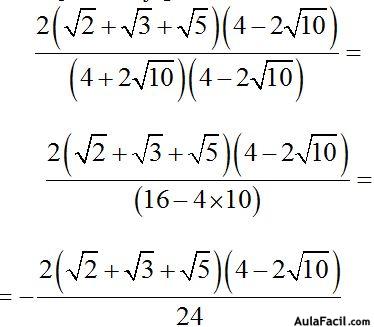
Simplificamos al numerador y denominador por 2:
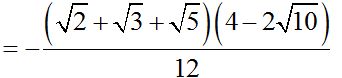
Para simplificar un producto de varios factores por un número, basta simplificar UN solo factor.
Podemos seguir simplificando al numerador y denominador, para ello, debo sacar factor común a 2 en 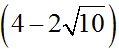 :
:
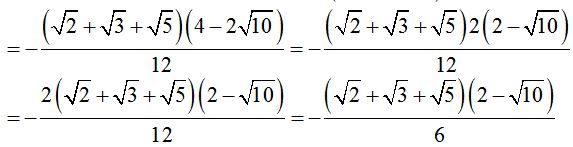
10.90 Racionaliza:
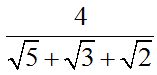 Respuesta:
Respuesta: 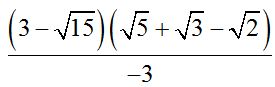 .
.
HALLAR LA RAÍZ CUADRADA DE UN POLINOMIO.
No es una operación que se utilice con frecuencia. Es bueno que conozcas el modo de extraer la raíz cuadrada de polinomio.
Hallar la raíz cuadrada de un monomio es tarea muy sencilla:
basta hallar la raíz de cada factor: de la parte numérica, si la tiene, y de la parte literal dividiendo cada exponente de cada factor entre 2 por tratarse de una raíz cuadrada.
10.91 Halla la raíz cuadrada de:
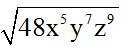 Respuesta:
Respuesta: 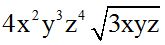 .
.
Solución:
De cada factor extraemos todo lo que podamos. Como 48 es igual a 16 x 3, del factor 16 podemos sacar fuera de la raíz cuadrada a 4.
Siempre que el exponente de la cantidad subradical sea mayor que el índice de la raíz dividimos, el exponente entre el índice, el cociente indica el exponente del factor fuera de la raíz y el resto es el exponente de ese factor dentro de la raíz:
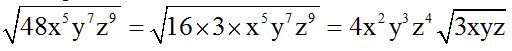
10.92 Halla la raíz cuadrada de: 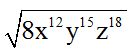
Respuesta: 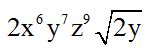 .
.
Vamos a hallar la raíz cuadrada de un polinomio:
1º Tenemos cuidado de que se encuentre ordenado respecto a una letra y en orden descendente:
Ejemplo:
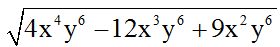
Tenemos el radicando ordenado respecto a la ‘x’.
2º Calculamos la raíz cuadrada del primer término del polinomio y lo colocamos en el lugar correspondiente a su resultado:
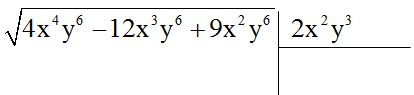
3º Elevamos al cuadrado el valor hallado y lo pasamos al radicando colocándolo debajo del primer término del radicando cambiándolo de signo. Sumamos y bajamos los dos términos siguientes:
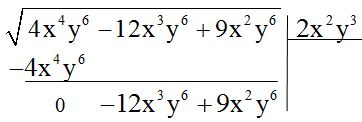
4º Hallamos el doble de la raíz calculada hasta ahora:
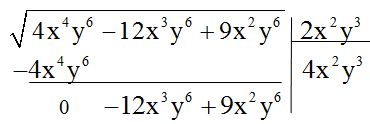
5º Dividimos el primero de los términos que ahora tenemos en el radicando entre el doble de la raíz hallada y su resultado, con el signo correspondiente, será el segundo término del resultado:
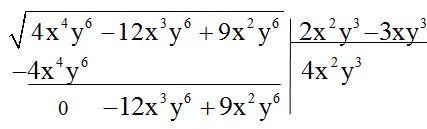
6º El último valor calculado lo colocamos a continuación del doble de la de la raíz que ya habíamos calculado:
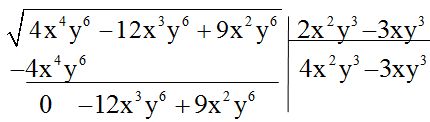
7º Los dos términos que componen: el doble de la raíz que había calculado al principio y el segundo término del resultado, los encierro entre paréntesis y los multiplico por este último valor:
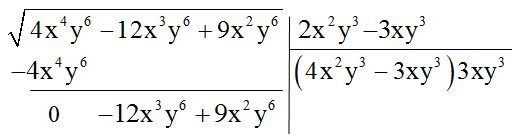
8º Realizo el producto que tengo indicado y los resultados que obtengo los cambio de signo y los coloco debajo de los dos términos que tengo en el radicando (los términos que bajé):
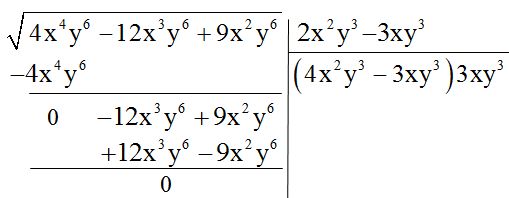
En el caso que tuviésemos más términos en el radicando, en este momento, bajaríamos los que se necesiten hasta completar tres términos.
Duplicaríamos la raíz calculada hasta el momento, colocando el resultado en una segunda nueva línea, debajo del doble de la raíz hallada anteriormente.
Dividiríamos el primer término del resto (radicando) entre el primer término del valor calculado en el paso anterior y este valor sería el tercer término de la respuesta.
Como comprobarás, vamos repitiendo los pasos explicados.
10.93 Calcular la raíz cuadrada de:
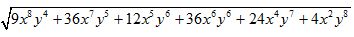
Respuesta: 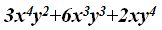 .
.
Solución:
Tienes hecha la raíz siguiendo los pasos indicados en el ejercicio anterior.
Al comprobar si estaba ordenado (respecto a ‘x’) el polinomio del radicando vemos que el tercero y cuarto términos no lo están. Corregimos su posición:
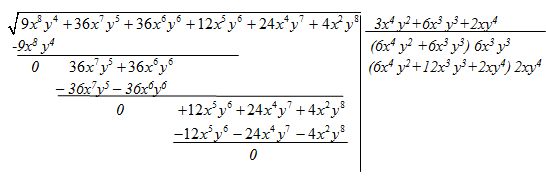
10.94 Calcular la raíz cuadrada de:
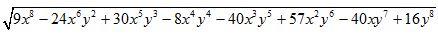
Respuesta: 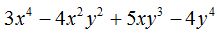 .
.
Solución:
Primero comprueba si el polinomio está debidamente ordenado.
Coloca debidamente los términos semejantes.
Tienes a continuación resuelta la raíz paso a paso:
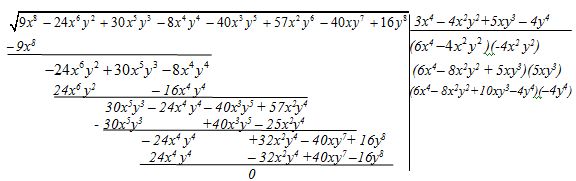
10.95 Calcula la raíz cuadrada de:
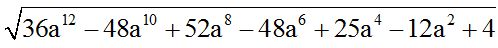
Respuesta: 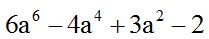 .
.

