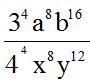Potencias y Raíces de Expresiones Algebraicas - Ejemplos
Supongamos que nos dicen que hagamos la siguiente operación:
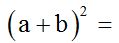
NUNCA se te ocurra elevar un sumando a una potencia. Cuando los términos están sumando o restando tienes que elevar la expresión a la potencia indicada, es decir, multiplicar por sí misma las veces que se indica en el exponente.
EJEMPLO:
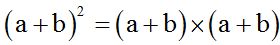
La suma a+b la tenemos que multiplicar por sí misma dos veces:
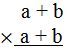
Hemos colocado las expresiones a multiplicar.
Comenzamos a multiplicar con la a del multiplicador. Cada término del multiplicador se multiplica por cada uno de los términos del multiplicando.
La a del multiplicador multiplica a cada uno de los términos del multiplicandor (a+b):
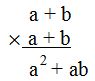
Ahora será la b del multiplicador quien multiplica a cada uno de los términos del multiplicando (a+b):
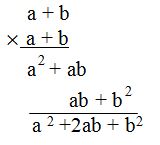
Guarda siempre el orden alfabético de las letras.
Los términos semejantes se colocan unos debajo de otros.
Recuerda que son semejantes los términos que tienen las mismas letras con los mismos exponentes.
Ejemplo: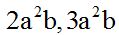 
No importa que la parte numérica de cada término sea diferente.
Una vez que hemos terminado de multiplicar, trazamos una raya por debajo y sumamos los términos que hemos calculado:
Para elevar una expresión algebraica a una potencia se eleva cada factor a dicha potencia y para elevar una potencia a otra se multiplican los exponentes.
Ejemplo: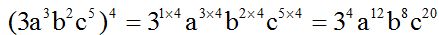 
Tanto la parte numérica como la parte literal está compuesta de factores.
10.46 Calcular:
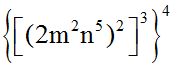Respuesta: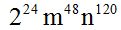 
Solución:
Para elevar una potencia a otra, se multiplican los exponentes.
CASO 2.- Monomios de base negativa:
10.47 Calcula:
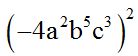Respuesta: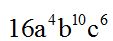 
Solución:
Cuando la base es negativa tienes que fijarte en el exponente al cual tenemos que elevar. Si el exponente es par, el resultado será positivo. Si es impar, el resultado será negativo:
Ejemplos:
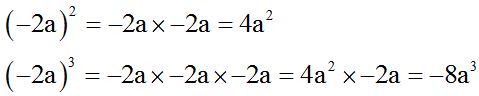
Si el número de factores con signo menos es par, el resultado es positivo y si es impar, el resultado es positivo
Para resolver estos ejercicios te basta con saber:
1º La regla de los signos en el producto y división:
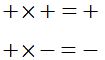y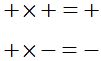 
2º Para multiplicar potencias de la misma base se suman los exponentes
3º Para elevar una potencia a otra se multiplican los exponentes.
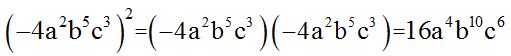
10.48 ¿Son iguales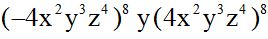 
?
Respuesta: Sí
Solución:
Son iguales porque cualquier potencia de base negativa o positiva y exponente par el resultado siempre es positivo.
10.49 Calcula:
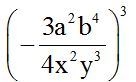Respuesta: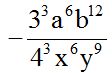 
Solución:
Recuerda que cuando el número de signos menos es impar, el resultado es negativo y positivo cuando el número de signos menos es par.
10.50 Calcula:
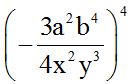Respuesta: 
