Logarítmos decimales o de Briggs - Logarítmos Neperianos - Ecuaciones Exponenciales
Los logaritmos decimales son los que has venido utilizando en los últimos ejercicios, que como se te dijo, cuando no escribimos la base, se entiende que es 10 el valor de la misma y la escribimos log.
Los logaritmos de base 10 se deben al matemático inglés de la universidad de Oxford, Henry Briggs el año 1624.
LOGARITMOS NEPERIANOS
Los primeros logaritmos se deben al matemático escocés John Napier o Neper hacia el año 1600. La base de estos logaritmos es un número irracional cuyo valor es:
2,7182818284590452354…
Recuerda que números irracionales son los que escribimos con infinitas cifras decimales y que, además, no son periódicas.
A esta base se la conoce con el nombre número e. Por lo tanto, base e o base 2,7182818284590452354…es lo mismo.
Los logaritmos neperianos se escriben: L(5) que significa logaritmo neperiano de 5 o logaritmo de 5 en base e o también, ln(5).
Debemos a Briggs el cambio a una base sencilla, no obstante, si sigues estudiando cursos superiores de matemáticas son los neperianos quienes tienen mayor importancia.
ECUACIONES EXPONENCIALES
Se llaman ecuaciones exponenciales a las que la incógnita aparece como exponente.
Ejemplo: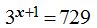 
Estas ecuaciones no son desconocidas para ti ya que hemos hecho uso al tratar los logaritmos.
17.34 Calcula el valor de x en la ecuación: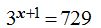 
Respuesta: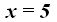 
Solución:
1) Esta ecuación podemos escribirla: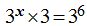 
Si dividimos por 3 a ambos miembros de la igualdad obtenemos: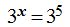 
Si las bases son iguales, también lo serán los exponentes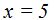 
2) Más fácil: Descomponiendo 729 en sus factores primos transformamos: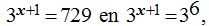 
de donde,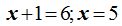 
17.35 Calcula el valor de n en la ecuación:
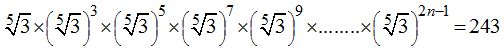
Respuesta: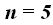 
Solución:
La ecuación del enunciado podemos escribirla: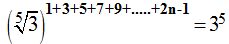 
Observo que el exponente: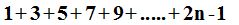 
son los términos de una progresión aritmética.
No conozco el valor del último término de una progresión de n términos en la que el primero vale 1 y la diferencia de la progresión 2.
Aplico la fórmula para conocer el valor del último término:
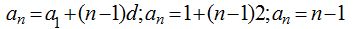
Haciendo uso de la fórmula de la suma de una progresión aritmética:
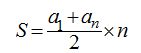
y sustituyendo por los valores numéricos que conocemos obtengo: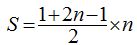 
de donde la suma vale: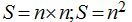 
Retomo la ecuación.
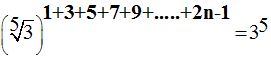
que puedo escribirla:
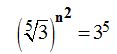
Transformo la raíz cuadrada en potencia y me queda:
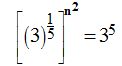
Elevando una potencia a otra: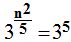 
Si las bases son iguales, también lo serán sus exponentes: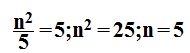 
17.36 En la ecuación: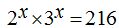 
¿Cuánto vale x?
Respuesta: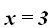 
Solución:
Recuerda que en un producto de dos potencias que tienen los mismos exponentes puedes multiplicar las bases dejando el mismo exponente: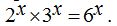 
17.37 Calcula el valor de x en la ecuación: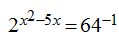 
Respuesta: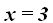 
17.38 Calcula el valor de x en la ecuación: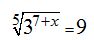 
Respuesta: 
17.39 Calcula el valor de x en la ecuación: 
Respuesta: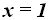 
17.40 Calcula los valores de x e y en el sistema:
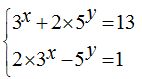
Respuestas: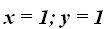 
17.41 Calcula los valores de x en la ecuación: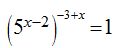 
Respuestas: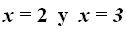 
17.42 Calcula los valores de x e y en el sistema:
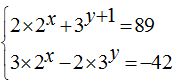
Respuestas: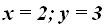 
17.43 Calcula los valores de x e y en el sistema:
Respuestas: 
17.44 Calcula los valores de x e y en el sistema:
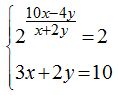
Respuestas: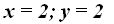 
17.45 Cuánto vale x en la ecuación:
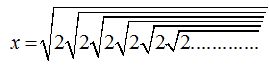
Respuesta: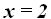 
Solución:
1) Se entiende que el número de raíces en el formato del enunciado son infinitas. ¿Crees que si al Océano Atlántico le quitas una gota de agua lo notarán los ecologistas?
Si tienes infinitas raíces, una menos, ni se nota.
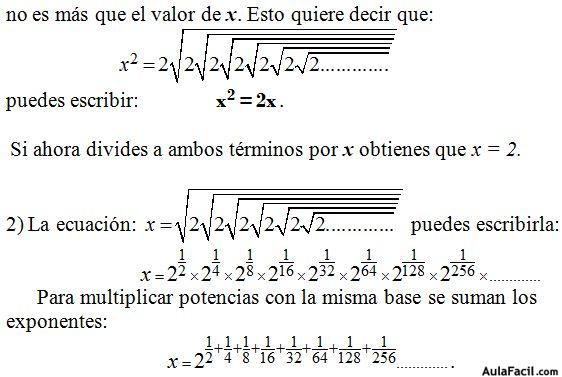
Si te fijas bien, el exponente es la suma de los infinitos términos de una progresión geométrica de razón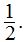 
El valor de la suma, en este caso, viene dada por:
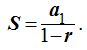
Reemplazando las letras por sus valores:
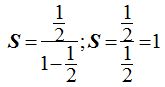
Vemos que: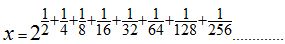 
podemos escribir como:
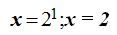
17.46 Calcula el valor de x en la ecuación: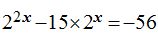 
Respuesta: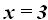 
Solución:
La ecuación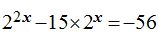 
podemos escribirla: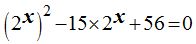 
Si a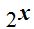 
le sustituimos por m tendremos: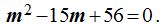 
Haciendo aplicación de:
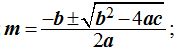
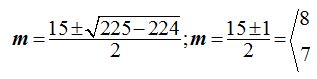
Tomando la solución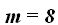 
vemos que 
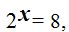es decir, de donde 
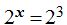de donde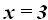 
Autor: Agradecemos a Don Ignacio Pujana el envío de este magnífico curso.
