Logaritmos Decimales
Se conocen con este nombre a los logaritmos cuya base es 10. Se escribe log sin indicar su base (se entiende que su ésta es 10).
17.19 Calcula el valor de x en la ecuación:
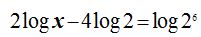
Respuesta: x = 32
Solución:
Lo resolvemos paso a paso.
17.20 Calcula el valor de x en la ecuación:
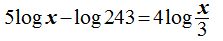
Respuesta: x = 3
17.21 Calcula el valor de x en la ecuación:
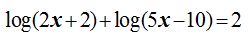
Respuesta: x = 4
17.22 Calcula el valor de x en la ecuación:
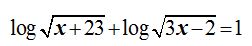
Respuesta: x = 2
Solución:
17.23 Halla el valor de x en la ecuación:
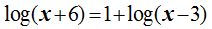
Respuesta: x = 4
17.24 ¿Cuánto vale el logaritmo de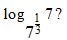 
Respuesta: 3
Solución:
Siendo x el valor del logaritmo de 7 en base 7 elevado a un tercio: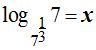 
puedo escribir teniendo en cuenta la definición de logaritmo y haciendo las operaciones correspondientes paso a paso:
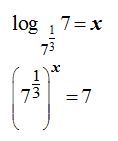
Lo que equivale a escribir: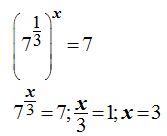 
17.25 ¿Cuánto vale el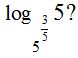 
Respuesta: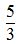 
17.26 ¿Podemos decir por lo visto en estos dos últimos ejercicios, que el logaritmo de la base elevado a un valor fraccionario la respuesta es el del valor fraccionario INVERTIDO?
Respuesta: SÍ
17.27 ¿Puedes asegurar que el 
es igual a cero?
Respuesta: SÍ porque el logaritmo de la unidad en cualquier base vale cero.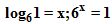 
y la unidad puedo escribirla como un número cualquiera (seis en este caso) elevado a cero. Este razonamiento puedo aplicarlo para cualquier valor numérico de la base.
17.28 Calcula los valores de x e y en el sistema:
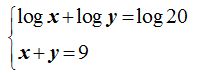
Respuestas: x=4 y x=5
Solución:
Cuando conozco el valor de la suma y el producto de dos números, para saber cuales son, recurro a la ecuación de 2º grado, en la que el coeficiente de (a) 
es 1, el coeficiente de(b) x el valor de la suma cambiada de signo y el valor del término independiente (c), el producto de ambos números.
La ecuación de segundo grado la escribo en función de la variable v (o cualquier otra que no sean x e y porque los valores que voy a obtener se refieren a estas incógnitas:
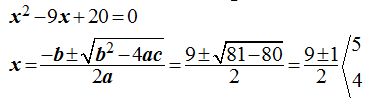
17.29 Calcula los valores de x e y en el sistema:
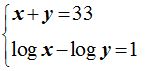
Respuestas: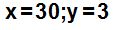 
Solución:
17.30 Calcula los valores de x e y en el sistema:
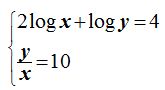
Respuestas: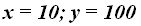 
Solución:
El sistema puedo escribirlo:
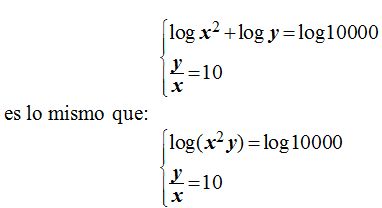
Elimino los logaritmos quedándome y haciendo operaciones en la segunda ecuación:
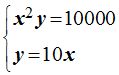
Sustituyo y en la primera ecuación por el valor que vemos que tiene en la segunda ecuación:
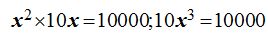
Simplificando ambos miembros del signo = por 10:
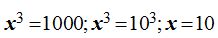
Sustituyo el valor conocido en la segunda ecuación:
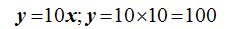
17.31 Calcula el valor de x en la ecuación:
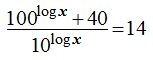
Respuesta: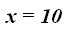 
Solución:
A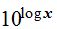 
le doy el valor m.
Esto quiere decir que,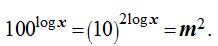 
De este modo consigo una expresión más sencilla: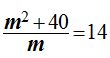 
Haciendo operaciones:
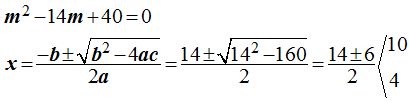
Tomamos la primera respuesta:
Si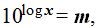 
podemos escribir: 
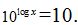Si las bases de ambas potencias son iguales también lo serán sus exponentes: 
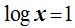y siguiendo la definición de logaritmo tendremos: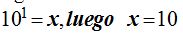 
17.32 Halla el valor de x en la ecuación:
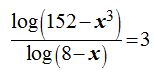
Respuestas: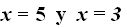 
Solución:
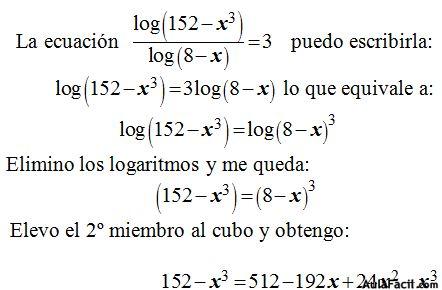
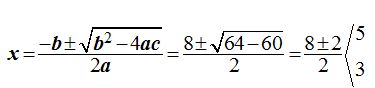
17.33 Resuelve el sistema:
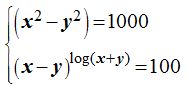
Respuestas: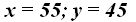 
Soluciones:
1ª Solución:
Resolvemos por deducción. Para ello, la 1ª ecuación escribimos:
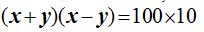
Si a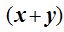 
le damos el valor 100, 
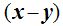tendrá el valor 10, y resolviendo el sistema:
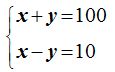
sumando las dos ecuaciones: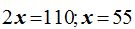 
Cambiando de signo a la segunda ecuación y sumándolas después: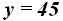 
2ª Solución:
Para facilitar cálculos a x+y le damos el valor a:
y a x-y le damos el valor b:
x+y= a
x-y=b
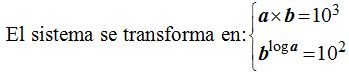
Despejamos a en la primera ecuación: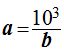 
En la segunda ecuación tomamos logaritmos y obtenemos:
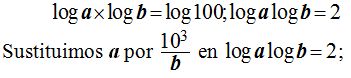
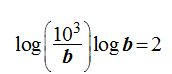
que es lo mismo que escribir teniendo en cuenta a qué es igual el logaritmo de un cociente:
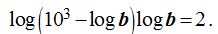
Quitando paréntesis:
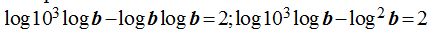
que a su vez podemos escribir:
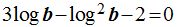
Si a log b le damos el valor m la última ecuación se nos ha transformado en:
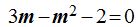
Como el término de grado 2 en la ecuación de 2º grado ha de ser positivo y ordenando la última ecuación, tenemos:
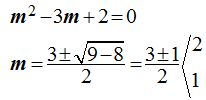
Si a log b le damos el valor 1: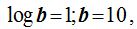 
es decir,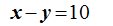 
Si a log a le damos el valor 2;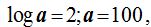 
es decir,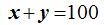 
y a partir de aquí, los valores de ambas incógnitas nos es muy sencillo calcularlas: 
