¿Porqué decimos que tres puntos no situados en la misma recta determinan un solo plano?
La contestación la encuentras en tu casa seguramente. Una silla que tiene 4 patas, puede determinar 2 planos, incluso más. Es suficiente que una de las patas sea un poco más larga o más corta que las demás.
Dado que las patas no están situadas en la misma recta determinan, en el caso de que una sola de las patas sea de distinta longitud, dos planos.
¿Cómo lo puedes comprobar? Observarás que una de las patas no toca el suelo y al sentarte sobre ella y moverte, notarás un pequeño vaivén que se produce al pasar del contacto de tres patas al contacto de tres pero una de ellas distinta al caso anterior.
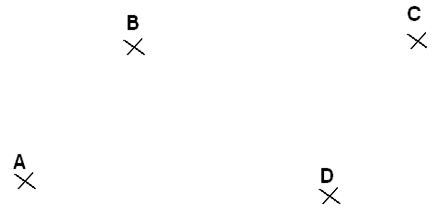
Supongamos que el punto de contacto de las patas de la silla con el suelo sean los puntos A, B, C y D.
Vamos a suponer que la pata correspondiente al punto B no tenga la misma longitud, que sea más corta que las otras tres que miden igual.
Verás que cuando haces apoyar esta pata, crearás un plano con los punto A, B y C (recuerda que 3 puntos no situados en línea recta determinan un plano).
El punto D corresponderá a otro plano, por eso no hace contacto con el suelo.
Si ahora haces apoyar la pata correspondiente al punto D crearás el plano A, C y D.
Diremos que la silla “cojea” al pasar de un plano a otro.
En la siguiente figura verás los dos planos en distintos colores:
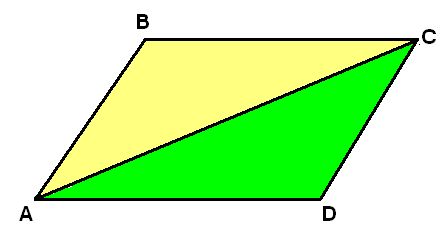
TRES PUNTOS SIEMPRE DETERMINAN UN SOLO PLANO
No olvides que tres puntos no situados en línea recta determinan un solo plano aunque las patas no tengan la misma longitud o el suelo no sea plano.
Puedes hacer la prueba con tres dedos de tu mano puestos verticales y separados. Coloca un libro sobre ellos y notarás que no se cae. Los tres dedos son los tres puntos que determinan un plano.
Es importante cuanto se relaciona con objetos que tienen tres patas, tres pies, etc., que los llamamos trípodes (tri tanto en griego como en latín significa tres y podo que significa pie).
Estos objetos se utilizan como soporte de aparatos que se usan para múltiples usos de precisión.
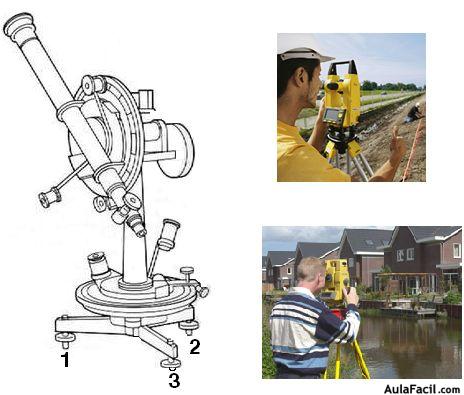
A continuación tienes una fotografía de un trípode:

Cuando se necesitan ciertos tipos de fotografías, el trípode se utiliza para colocar la cámara sobre ella. Estaremos seguros que no tendrá ningún movimiento porque los tres puntos de apoyo determinan un solo plano.
Otro aparato que necesita de trípode es el teodolito(instrumento que sirve para mediciones de mucha precisión a distancia) que puedes apreciar en la siguiente figura. Se trata de un teodolito muy antiguo. Apreciarás que descansa sobre tres puntos. Aunque el suelo no sea liso, tres puntos determinan un plano.
En las otras dos fotografías, teodolitos más modernos siendo usados en medición de terrenos: