Representación de los Valores de una Función

Se trata de algo muy sencillo, representar sobre el eje de abscisas los valores de una función.

Con un ejemplo resuelto será suficiente para que lo entiendas.
 
Supongamos el ejercicio siguiente:

27.30 ¿ Cuál es el dominio de ?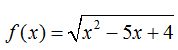

Solución

Resolvemos la ecuación de 2º grado: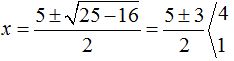 

Vemos que todos los valores comprendidos entre (1,4), es decir: 

2 y 3 hacen que el radicando sea negativo, en cambio, con el resto de valores será positivo.

Si es negativo el valor de sustitución no es válido, porque no existe una raíz de índice par que sea negativa.

Cuanto acabamos de decir lo llevamos a un eje de abscisas:

Fijamos los valores:

Fíjate que tenemos dos grupos de valores que son válidos. 

Unimos estos dos grupos con su símbolo correspondiente U (unión de ambos grupos válidos).

No necesitamos indicar que los elementos de x pertenecen a un conjunto determinado porque ya especificamos sus valores concretos.

Respuesta: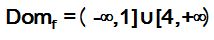 

27.31 Calcula el dominio de la función: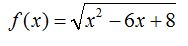 

Respuesta: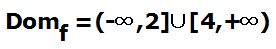 

27.32 ¿ Cuál es el dominio de la función :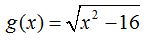 

Respuesta: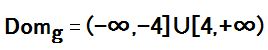 

Solución

El radicando ha de ser positivo, por lo tanto,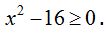 

Pasando – 16 a la derecha de la inecuación 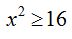 de donde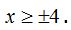 

Llevamos estos valores a la recta de abscisas:

27.33 Calcula el dominio de la función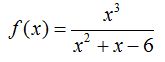 

Respuesta: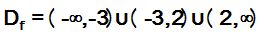 

Solución

Como en otras ocasiones, hallamos las raíces del denominador: 

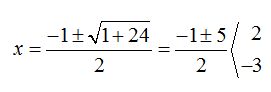
Comprobamos que – 3 y 2 son los valores que hacen que el denominador valga cero, es decir, no nos interesan. El resto de los valores reales son válidos y los representamos sobre la recta:

En verde, los valores del dominio de la función.

En rojo, los dos valores que hemos de excluirlos.

Podemos escribir que el 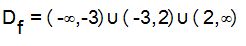.