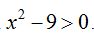Dominio de las Funciones Logaritmicas
Sabemos que el logaritmo de un número es el exponente al que hemos de elevar la base para obtener el número.
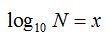
En el ejemplo:
la base es 10
el número es N
el logaritmo es x
Según la definición tendremos: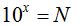
La base ha de ser positiva y mayor que cero: 10,2.71,0,2.
¿Puede valer la base de los logaritmos menos que 1, es decir, 0<base<1?
Sí y vamos a demostrarlo cambiando la base de los logaritmos a un número menor que 1, por ejemplo, 0,43.
Supongamos que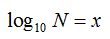 
, esto significa que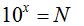 
Imaginemos que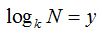 
, lo que significa: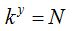 
Observamos que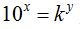 
porque ambos son iguales a N.
Tomamos logaritmos en los dos miembros de la igualdad en base 10:
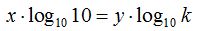
Despejamos y (logaritmo en la nueva base):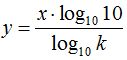 
Sabemos que el logaritmo de la base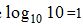 
, lo mismo que 
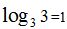, etc. por ello: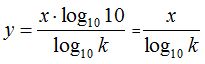 
Sustituyendo el valor de x:y =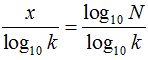 
Ejemplo:
¿Cuál es el logaritmo de 2 en base 0,43?
Respuesta: log(2) / log(0,43) = -0,821293556
El número del cual calculamos su logaritmo debe ser positivo > 0, no existen logaritmos de números negativos.
Existen logaritmos negativos cuando los números son positivos y menores que la unidad, ejemplos: log(0,3) = -0,522878745 log(0,0021)= -2,67778071
Los logaritmos se hallan de números reales y positivos lo que significa que su dominio será: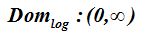
Acabamos de indicar: “el dominio puede ser…” porque en cada caso convendrá analizar:
27.34 Halla el dominio de la función: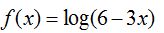 
Respuesta: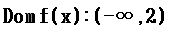 
Solución
La cantidad que tienes entre paréntesis 6-3x debe valer >0 porque no podemos tomar logaritmos ni de cero ni de números negativos.
log(6-3x)>0, es decir, 6>3x, , simplificando:2>x.
Observa que al 2 no lo tenemos en cuenta porque no podemos tomar logaritmos de 0.
27.35 Calcula el dominio de la función f(x)= log(x+2)
Respuesta: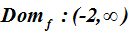 
Solución
El número del que obtenemos el logaritmo debe ser mayor que 0, (x+2)>0.
Veamos que x ha de ser mayor que -2: x>-2 por lo que el dominio será:
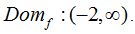
27.36 Calcula el dominio de la función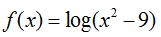 
Respuesta: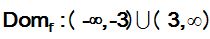 
Solución
Veamos que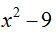 
debe ser mayor que cero.
Como x está elevado al cuadrado, sea cual fuere el signo del valor de la variable, al sustituir en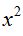 
será positivo.
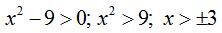
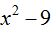será positivo siempre que x esté comprendido en el intervalo 
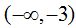,por un lado, y por otro,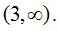 
Los valores situados en el intervalo con línea roja no cumplen con la inecuación 
