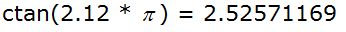Dominio de la Tangente y Dominio de la Cotangente
Si queremos determinar el dominio de la tangente hemos de tener en cuenta que
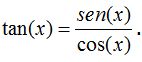
Esto quiere decir que el cos(x) no debe tomar el valor 0. Es decir, has de evitar el 0 del denominador.
¿Cuándo el cos(x) vale 0?
(Los ángulos expresados con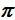 
nos referimos a su medida en radianes). Por si no recuerdas, un radián equivale a un ángulo cuyo arco mide la longitud del radio. Una circunferencia completa tiene 2
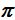radianes.
Aprendimos en Trigonometría que el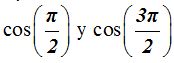 
valen 0.
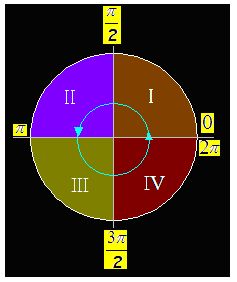
La circunferencia trigonométrica tiene un radio igual a 1, es decir, su longitud equivale a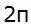 
.Como la tenemos dibujada en el centro de coordenadas, cada cuadrante equivale a 
.
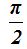Lo podemos comprobar en la pantalla de Google:
En el tercer cuadrante: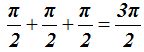
también vale cero.
Supongamos un ángulo superior a 360º, por ejemplo 450º quiere decir que damos una vuelta completa más 90º: 360º + 90º = 450º y como 90º equivale a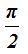 
tendríamos: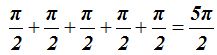 
Veamos en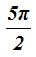 
también el coseno vale 0.
Si a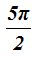 
le sumas dos cuadrantes: 
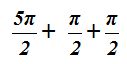sumando obtenemos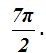 
Los cosenos de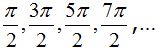 
que como ves, se tratan de coeficientes impares de 
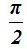valen 0.
El dominio de la tangente lo podemos escribir según lo que acabamos de estudiar:
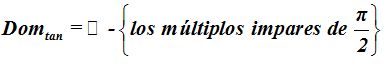
Dominio de la cotangente
Sabemos que el valor de la ctan, cotang, cotg,… procede de dividir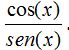 
Como ves, el sen(x) no debe tomar el valor 0.
Por otra parte, estudiamos anteriormente que
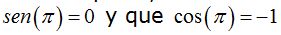lo quiere decir que 
,
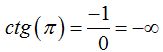es decir, no existe.
Cualquier múltiplo de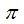 
no participa del dominio de la cotangente por no ser un número real. Por todo esto podemos decir que:
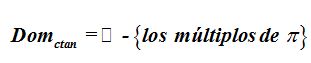
Quizá no estaría mal agregar, aunque no sea imprescindible la matización:
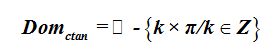
El dominio comprende los números reales menos los múltiplos de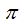 
con tal de que k sea un número entero.
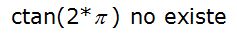
En cambio: 
