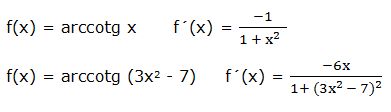Teoría: Derivadas trigonométricas

a) Derivada del seno:

La derivada del seno de una función “w” es la derivada de esa función por el coseno de dicha función:

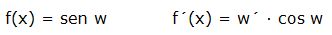
Ejemplo: 

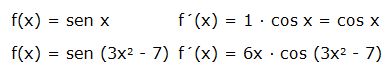
c) Derivada de la tangente:

La derivada de la tangente de una función “w” es igual a la derivada de la función dividida por el coseno al cuadrado de dicha función:

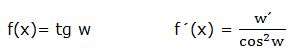
Ejemplos:

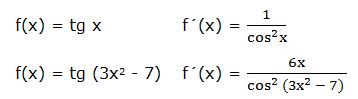
A partir de la definición de la tangente podríamos llegar a la definición anterior:

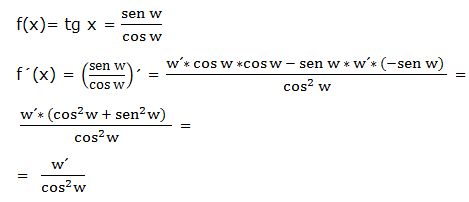
Partiendo de la definición anterior, y aplicando reglas trigonométricas, podemos definir la derivada de la tangente de una función de las siguientes formas:

d) Derivada de la cosecante:

La derivada de la cosecante de una función “w” es igual a la derivada de la función con signo negativo por el coseno de la función dividido por su seno al cuadrado:

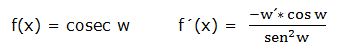
Ejemplo:

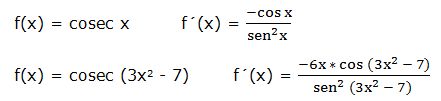
Aplicando las reglas trigonométricas esta derivada también la podemos definir:

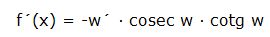
e) Derivada de la secante:

La derivada de la secante de una función “w” es igual a la derivada de la función por el seno de la función dividido por su coseno al cuadrado de la función:

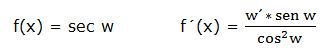
Ejemplos: 

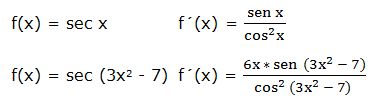
Aplicando las reglas trigonométricas también la podemos definir:

f) Derivada de la cotangente:

La derivada de la cotangente de una función “w” es igual a la derivada de la función con signo negativo dividida por el seno al cuadrado de dicha función:

Ejemplo:

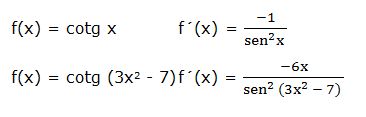
Aplicando las reglas trigonométricas también la podemos definir:

DERIVADAS TRIGONOMÉTRICAS INVERSAS

a) Derivada del arcoseno:

La derivada del arcoseno de una función “w” es igual a la derivada de la función dividida por la raíz cuadrada de 1 menos la función al cuadrado:

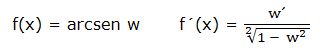
Ejemplos: 

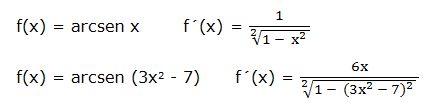
b) Derivada del arcocoseno:

La derivada del arcocoseno de una función “w” es igual a la derivada de la función con signo negativo dividida por la raíz cuadrada de 1 menos la función al cuadrado:

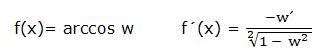
Ejemplo:

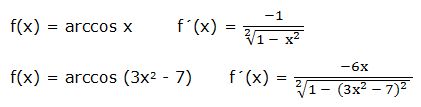
c) Derivada del arcotangente:

La derivada del arcotangente de una función “w” es igual a la derivada de la función dividida por 1 más la función al cuadrado:

Ejemplo:

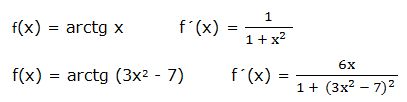
d) Derivada del arcocosecante: 

La derivada del arcocosecante de una función “w” es igual a menos la derivada de la función dividida por el producto de la función por la raíz cuadrada de la función al cuadrado menos 1:

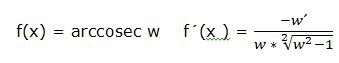
Ejemplo:

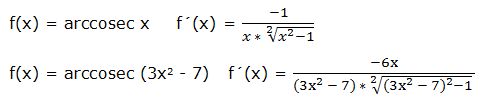
f) Derivada del arcocotangente:

La derivada del arcocotangente de una función “w” es igual a la derivada de la función con signo negativo dividida por 1 más la función al cuadrado:

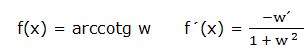
Ejemplo: