Teoría: Regla de la cadena
Cuando tenemos una función compuesta (una función dentro de otra función):
h(x) = g[f(x)]
Por ejemplo:
h(x) = ln (sen x)
Tenemos una función logarítmica g[f(x)] = ln a
Cuyo argumento “a” es un función de seno f(x) = sen x
La derivada de la función compuesta es:
h´(x) = g´[f(x)] * f´(x)
En el ejemplo anterior:
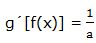; si sustituimos el argumento “a” por su valor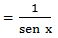 
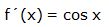
Luego:
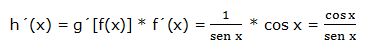
Veamos más ejemplos:
a) h(x) = sen x5
Tenemos una función de seno g[f(x)] = sen (a), siendo “a” una función potencia f(x) = x5.
La derivada de la función compuesta es:
g´[f(x)] = cos a; si sustituimos “a” por su valor = cos x5
f´(x) = 5x4
Luego:
h´(x) = g´[f(x)] * f´(x) = cos x5 * 5x4
b) h(x) = (4x3 + 2x2 – 3x)5
Tenemos una función potencia g[f(x)] = a5, siendo la base “a” una función polinómica f(x) = (4x3 + 2x2 – 3x).
La derivada de la función compuesta es:
h´(x) = g´[f(x)] * f´(x)
Por tanto:
g´[f(x)] = 5a4 ; si sustituimos ”a” por su valor = 5 * (4x3 + 2x2 – 3x)4
f´(x) = (12x2 + 4x– 3)
Luego:
h´(x) = g´[f(x)] * f´(x) = 5 * (4x3 + 2x2 – 3x)4 * (12x2 + 4x– 3)
c)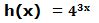 
Tenemos una función exponencial g[f(x)] = 4a cuyo exponente “a” es una función polinómica f(x) = 3x.
La derivada de la función compuesta es:
h´(x) = g´[f(x)] * f´(x)
Por tanto:
g´[f(x)] = 4a * ln 4; si sustituimos ”a” por su valor =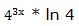 
f´(x) = 3
Luego:
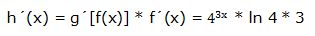
d) h(x) = tg (ln x)
Tenemos una función tangente g[f(x)] = tg (a), siendo “a” una función logarítmica f(x) = ln x.
La derivada de la función compuesta es:
h´(x) = g´[f(x)] * f´(x)
Por tanto:
Luego:
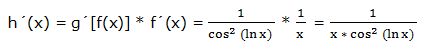
e) h(x) = sen 23x
Tenemos una función seno g[f(x)] = sen (a), siendo “a” una función exponencial f(x) = 23x.
La derivada de la función compuesta es:
h´(x) = g´[f(x)] * f´(x)
Por tanto:
Luego:
h´(x) = g´[f(x)] * f´(x) = cos 23x * 3 * 23x * ln 2
f) h(x) = cos (cos 3x)
Tenemos una función coseno g[f(x)] = cos (a), siendo “a” a su vez otra función coseno f(x) = cos 3x.
La derivada de la función compuesta es:
h´(x) = g´[f(x)] * f´(x)
Por tanto:
Luego:
h´(x) = g´[f(x)] * f´(x) = -sen (cos 3x) * (-3) * sen 3x
