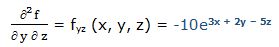Función de tres variables independientes

1.- f(x, y, z) = 5x⁴ + 3y² – 2z⁴

Primera derivada parcial respecto a “x”:

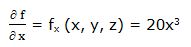
Segunda derivada parcial respecto a “x”:

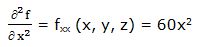
Primera derivada parcial respecto a “y”:

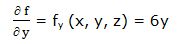
Segunda derivada parcial respecto a “y”:

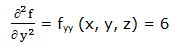
Primera derivada parcial respecto a “z”:

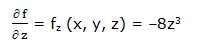
Segunda derivada parcial respecto a “z”:

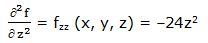
Segunda derivada respecto a “x” y respecto a “y”: Partimos de la primera derivada parcial respecto a “x” y la derivamos respecto a “y” (también podríamos haber partido de la primera derivada parcial respecto a “y” y derivar respecto a “x”).

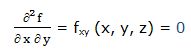
Segunda derivada respecto a “x” y respecto a “z”:

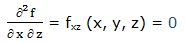
Segunda derivada respecto a “x” y respecto a “z”:

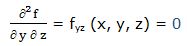
2.- f(x, y, z) = 5x²y⁴z³

Primera derivada parcial respecto a “x”:

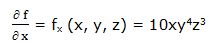
Segunda derivada parcial respecto a “x”:

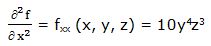
Primera derivada parcial respecto a “y”:

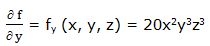
Segunda derivada parcial respecto a “y”:

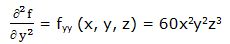
Primera derivada parcial respecto a “z”:

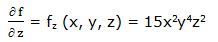
Segunda derivada parcial respecto a “z”:

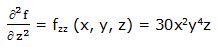
Segunda derivada respecto a “x” y respecto a “y”: Partimos de la primera derivada parcial respecto a “x” y la derivamos respecto a “y” (también podríamos haber partido de la primera derivada parcial respecto a “y” y derivar respecto a “x”).

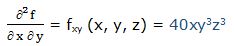
Segunda derivada respecto a “x” y respecto a “z”:

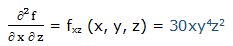
Segunda derivada respecto a “xy” y respecto a “z”:

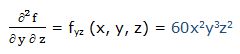
3.- f(x, y, z) = e^{3x + 2y – 5z}

Primera derivada parcial respecto a “x”:

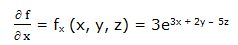
Segunda derivada parcial respecto a “x”:

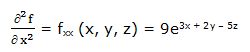
Primera derivada parcial respecto a “y”:

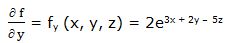
Segunda derivada parcial respecto a “y”:

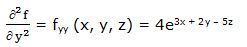
Primera derivada parcial respecto a “z”:

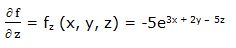
Segunda derivada parcial respecto a “z”:

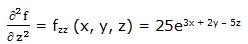
Segunda derivada respecto a “x” y respecto a “y”: Partimos de la primera derivada parcial respecto a “x” y la derivamos respecto a “y” (también podríamos haber partido de la primera derivada parcial respecto a “y” y la derivar respecto a “x”).

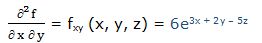
Segunda derivada respecto a “x” y respecto a “z”:

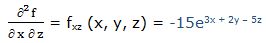
Segunda derivada respecto a “x” y respecto a “z”: