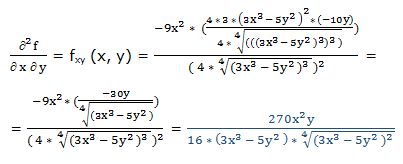Función de dos variables independientes

En una función con 2 variables independientes f(x, y) podemos derivar individualmente respecto a cada una de estas variables. Estaríamos calculando la primera derivada parcial de la función respecto a la variable utilizada. La otra variable se comportaría como una constante.

Para calcular estas derivadas parciales se aplican las mismas fórmulas que hemos utilizado en las derivadas de funciones con una sola variable independiente.

1ª derivada parcial de la función f (x, y) respecto a la variable independiente “x”:

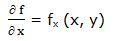
1ª derivada parcial de la función f (x, y) respecto a la variable independiente “y”:

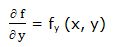
Si volviéramos a derivar la primera derivada parcial de la función respecto a la variable utilizada obtendríamos la segunda derivada:

2ª derivada parcial de la función f (x, y) respecto a la variable independiente “x”:

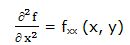
2ª derivada parcial de la función f (x, y) respecto a la variable independiente “y”:

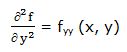
Si la primera derivada parcial respecto a la variable “x” la deriváramos respecto a la variable “y” obtendríamos la derivada cruzada de la función f (x, y) respecto a ambas variables, también denominada derivada segunda de la función con respecto a las variables “x” e “y”:

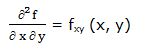
ATENCIÓN: obtendríamos el mismo resultado si deriváramos primero respecto a la variable “x” y luego respecto a la variable “y” que si lo hiciéramos en el orden inverso, primero sobre la variable “y” y luego sobre la variable “x”.

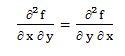
EJERCICIOS

1.- f(x, y) = 4x³ + 5y²

Primera derivada parcial respecto a “x”:

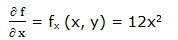
Segunda derivada parcial respecto a “x”:

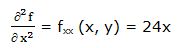
Primera derivada parcial respecto a “y”:

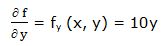
Segunda derivada parcial respecto a “y”:

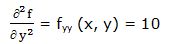
Segunda derivada respecto a “x” y respecto a “y”: Partimos de la primera derivada parcial respecto a “x” y la derivamos respecto a “y” (también podríamos haber partido de la primera derivada parcial respecto a “y” y la derivar respecto a “x”).

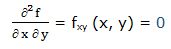
2.- f(x, y) = 5x - 3y⁴

^​Primera derivada parcial respecto a “x”:

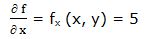
Segunda derivada parcial respecto a “x”:

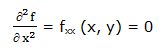
Primera derivada parcial respecto a “y”:

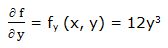
Segunda derivada parcial respecto a “y”:

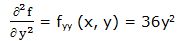
Segunda derivada respecto a “x” y respecto a “y”:

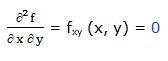
3.- f(x, y) = 6y - 2y³

Primera derivada parcial respecto a “x”:

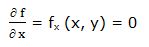
Segunda derivada parcial respecto a “x”:

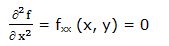
Primera derivada parcial respecto a “y”:

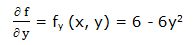
Segunda derivada parcial respecto a “y”:

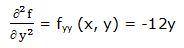
Segunda derivada respecto a “x” y respecto a “y”:

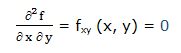
4.- f(x, y) = 7x³ + 5x² + 4

Primera derivada parcial respecto a “x”:

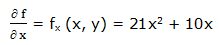
Segunda derivada parcial respecto a “x”:

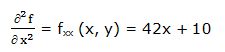
Primera derivada parcial respecto a “y”:

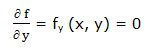
Segunda derivada parcial respecto a “y”:

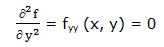
Segunda derivada respecto a “x” y respecto a “y”:

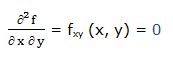
5.- f(x, y) = 5xy - 3

Primera derivada parcial respecto a “x”:

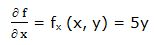
Segunda derivada parcial respecto a “x”:

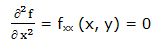
Primera derivada parcial respecto a “y”:

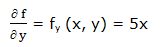
Segunda derivada parcial respecto a “y”:

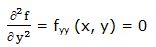
Segunda derivada respecto a “x” y respecto a “y”:

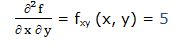
6.- f(x, y) = 4x³y²

Primera derivada parcial respecto a “x”:

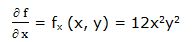
Segunda derivada parcial respecto a “x”:

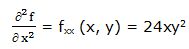
Primera derivada parcial respecto a “y”:

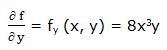
Segunda derivada parcial respecto a “y”:

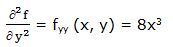
Segunda derivada respecto a “x” y respecto a “y”:

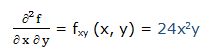
7.- f(x, y) = 4x³y² + 3x³ + 2y - 6

Primera derivada parcial respecto a “x”:

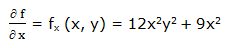
Segunda derivada parcial respecto a “x”:

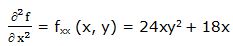
Primera derivada parcial respecto a “y”:

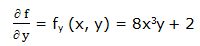
Segunda derivada parcial respecto a “y”:

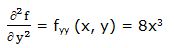
Segunda derivada respecto a “x” y respecto a “y”:

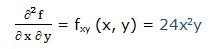
8.- f(x, y) = 7x²y² – 2xy+ 3

Primera derivada parcial respecto a “x”:

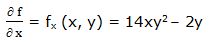
Segunda derivada parcial respecto a “x”:

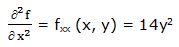
Primera derivada parcial respecto a “y”:

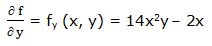
Segunda derivada parcial respecto a “y”:

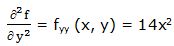
Segunda derivada respecto a “x” y respecto a “y”:

9.- f(x, y) = 8x³y – 4xy² + 3x² – 4y²

Primera derivada parcial respecto a “x”:

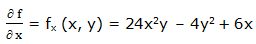
Segunda derivada parcial respecto a “x”:

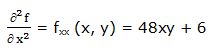
Primera derivada parcial respecto a “y”:

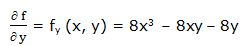
Segunda derivada parcial respecto a “y”:

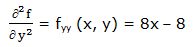
Segunda derivada respecto a “x” y respecto a “y”:

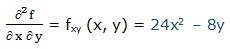
10.- f(x, y) = 2x³ * (5xy³ + 3xy)

Primera derivada parcial respecto a “x”:

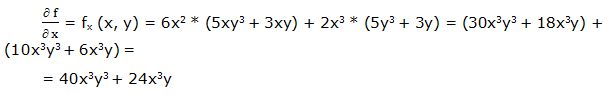
Segunda derivada parcial respecto a “x”:

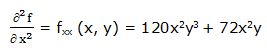
Primera derivada parcial respecto a “y”:

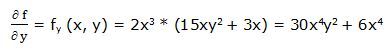
Primera derivada parcial respecto a “y”:

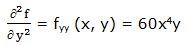
Segunda derivada respecto a “x” y respecto a “y”:

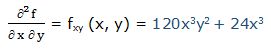
11.- f(x, y) = 4xy * (4x²y+ 2y)

Primera derivada parcial respecto a “x”:

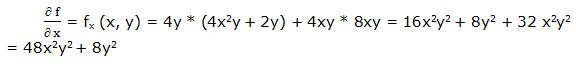
Segunda derivada parcial respecto a “x”:

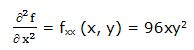
Primera derivada parcial respecto a “y”:

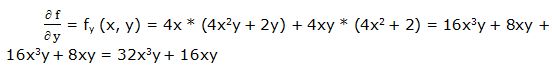
Segunda derivada parcial respecto a “y”:

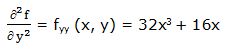
Segunda derivada respecto a “x” y respecto a “y”:

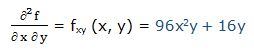
12.- f(x, y) = 5x² * (7x² – 3y²)

Primera derivada parcial respecto a “x”:

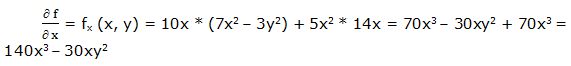
Segunda derivada parcial respecto a “x”:

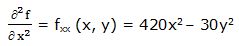
Primera derivada parcial respecto a “y”:

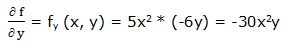
Segunda derivada parcial respecto a “y”:

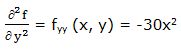
Segunda derivada respecto a “x” y respecto a “y”:

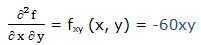
13.- f(x, y) = 4y² * (2x³ + 4y)

Primera derivada parcial respecto a “x”:

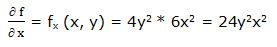
Segunda derivada parcial respecto a “x”:

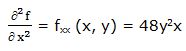
Primera derivada parcial respecto a “y”:

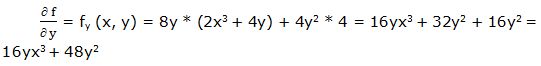
Segunda derivada parcial respecto a “y”:

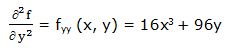
Segunda derivada respecto a “x” y respecto a “y”:

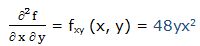
14.- f(x, y) = (5x- 2y) * (3x+ 4)

Primera derivada parcial respecto a “x”:

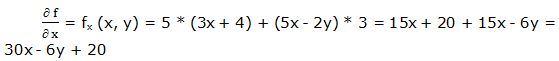
Segunda derivada parcial respecto a “x”:

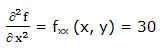
Primera derivada parcial respecto a “y”:

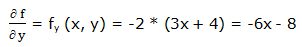
Segunda derivada parcial respecto a “y”:

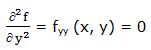
Segunda derivada respecto a “x” y respecto a “y”:

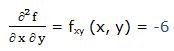
15.- f(x, y) = (2x+ 3y) * (5x+ 7y)

Primera derivada parcial respecto a “x”:

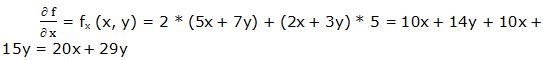
Segunda derivada parcial respecto a “x”:

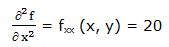
Primera derivada parcial respecto a “y”:

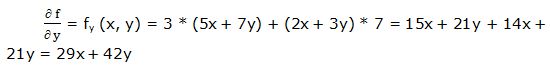
Segunda derivada parcial respecto a “y”:

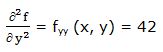
Segunda derivada respecto a “x” y respecto a “y”:

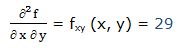
16.- f(x, y) = (3x² + 5y³) * (4x³ - 2y⁵)

Primera derivada parcial respecto a “x”:

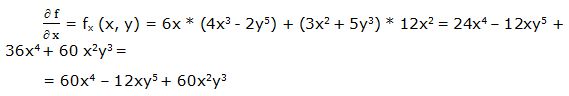
Segunda derivada parcial respecto a “x”:

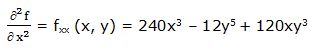
Primera derivada parcial respecto a “y”:

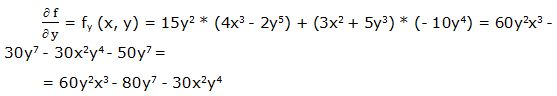
Segunda derivada parcial respecto a “y”:

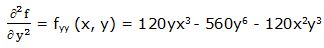
Segunda derivada respecto a “x” y respecto a “y”:

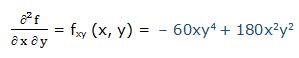
17.- f(x, y) = (3y² + 2xy) * (2x⁴ - 3x²y)

Primera derivada parcial respecto a “x”:

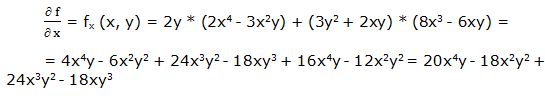
Segunda derivada parcial respecto a “x”:

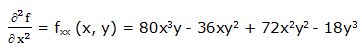
Primera derivada parcial respecto a “y”:

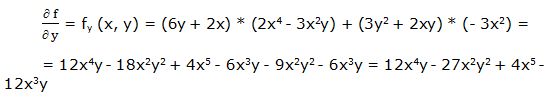
Segunda derivada parcial respecto a “y”:

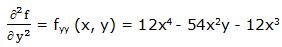
Segunda derivada respecto a “x” y respecto a “y”:

18.- f(x, y) = e^x + e^Y

Primera derivada parcial respecto a “x”:

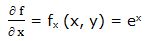
Segunda derivada parcial respecto a “x”:

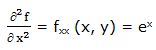
Primera derivada parcial respecto a “y”:

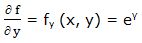
Segunda derivada parcial respecto a “y”:

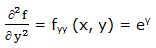
Segunda derivada respecto a “x” y respecto a “y”:

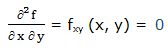
19.- f(x, y) = e^3XY + e^2Y

Primera derivada parcial respecto a “x”:

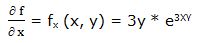
Segunda derivada parcial respecto a “x”:

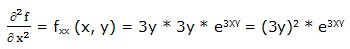
Primera derivada parcial respecto a “y”:

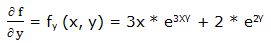
Segunda derivada parcial respecto a “y”:

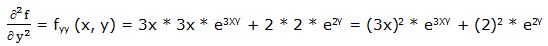
Segunda derivada respecto a “x” y respecto a “y”:

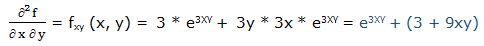
20.- f(x, y) = 5^3XY + xy² + 3x⁴ - 5y²

Primera derivada parcial respecto a “x”:

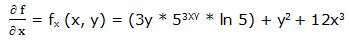
Segunda derivada parcial respecto a “x”:

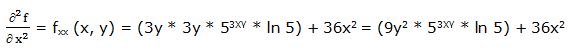
Primera derivada parcial respecto a “y”:

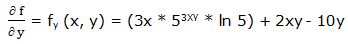
Segunda derivada parcial respecto a “y”:

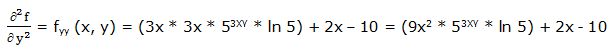
Segunda derivada respecto a “x” y respecto a “y”:

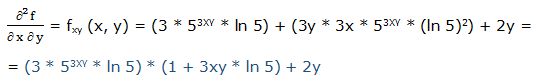
21.- f(x, y) = y * sen x

Primera derivada parcial respecto a “x”:

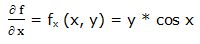
Segunda derivada parcial respecto a “x”:

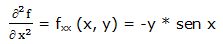
Primera derivada parcial respecto a “y”:

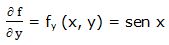
Segunda derivada parcial respecto a “y”:

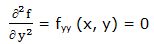
Segunda derivada respecto a “x” y respecto a “y”:

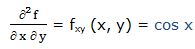
22.- f(x, y) = sen (x²) * cos (y²)

Primera derivada parcial respecto a “x”:

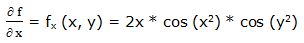
Segunda derivada parcial respecto a “x”:

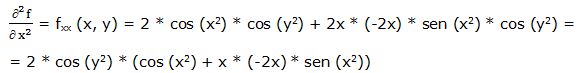
Segunda derivada parcial respecto a “x”:

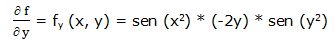
Segunda derivada parcial respecto a “y”:

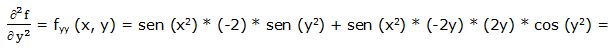
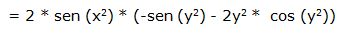
Segunda derivada respecto a “x” y respecto a “y”:

23.- f(x, y) = sen (3x⁴ + 2y²)

Primera derivada parcial respecto a “x”:

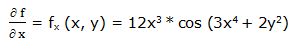
Segunda derivada parcial respecto a “x”:

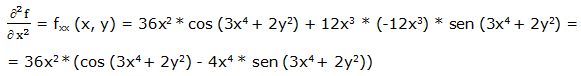
Primera derivada parcial respecto a “y”:

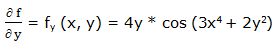
Segunda derivada parcial respecto a “y”:

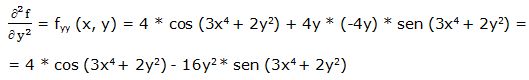
Segunda derivada respecto a “x” y respecto a “y”:

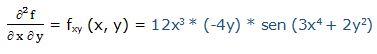
24.- f(x, y) = ln (5x² - 3y)

Primera derivada parcial respecto a “x”:

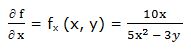
Segunda derivada parcial respecto a “x”:

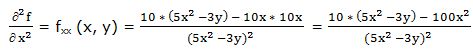
Primera derivada parcial respecto a “y”:

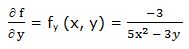
Segunda derivada parcial respecto a “y”:

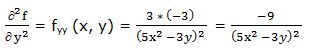
Segunda derivada respecto a “x” y respecto a “y”:

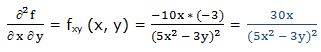
25.- f(x, y) =  

Primera derivada parcial respecto a “x”:

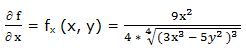
Segunda derivada parcial respecto a “x”:

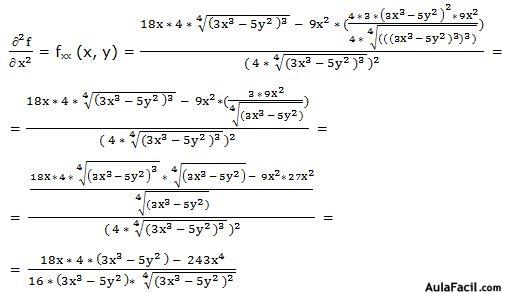
Primera derivada parcial respecto a “y”:

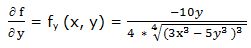
Segunda derivada parcial respecto a “y”:

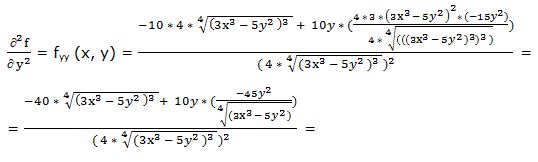
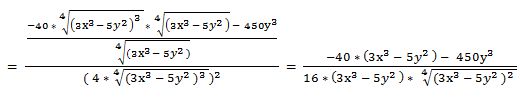
Segunda derivada respecto a “x” y respecto a “y”: