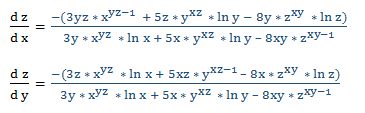Derivada de una función implícita

Mientras que en una función explícita la variable independiente se localiza en uno de los términos y la variable dependiente en el otro:

y = f(x)

Por ejemplo:

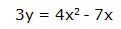
En la función implícita ambas variables se localizan en el mismo término:

F(x, y) = 0

Por ejemplo:

5y - 3x² = 0

Para derivar una función implícita hay tres posibilidades:

a) Despejar la variable dependiente “y” y derivar como una función normal:

Por ejemplo:

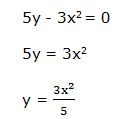
Y ahora derivaríamos como una función explícita.

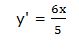
b) Derivar utilizando las reglas habituales y a continuación despejar y'.

Sabemos que x' = 1

En cambio la variable dependiente “y”, su derivada es la que estamos calculando y no tiene por qué ser igual a 1, por ello la dejaremos indicada como y'.

Una vez derivada la función despejaremos y'.

Por ejemplo:

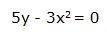
Derivamos:

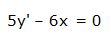
Y despejamos:

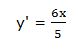
c) En funciones más complejas es útil aplicar la siguiente regla:

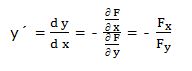
Siendo:

F_x la derivada de la función F (x, y) respecto a la variable independiente “x”

F_y la derivada de la función F (x, y) respecto a la variable dependiente “y”

Para aplicar esta fórmula se tiene que cumplir que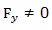 

Por ejemplo:

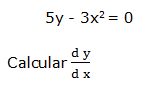
Escribimos la función en la forma: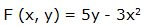 

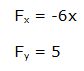
Luego:

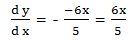
Este es el método que vamos a utilizar en los siguientes ejemplos.

Ejercicios

1.- Dada la función: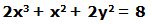 

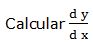
Pasamos todos los términos al miembro de la izquierda y escribimos la función en la forma:

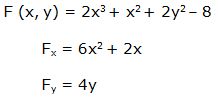
Luego:

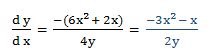
Vamos a derivar nuevamente esta función utilizando el segundo procedimiento indicado:

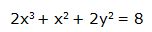
Derivamos:

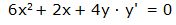
Despejamos:

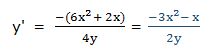
2.- Dada la función: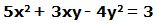  

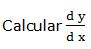
Escribimos la función en la forma: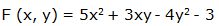 

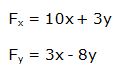
Luego:

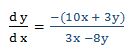
3.- Dada la función: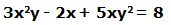  

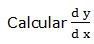
Escribimos la función en la forma: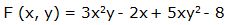 

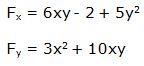
Luego:

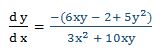
4.- Dada la función: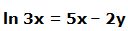 

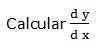
Escribimos la función en la forma: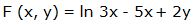 

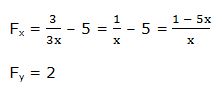
Luego:

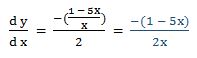
5.- Dada la función: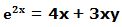  

Escribimos la función en la forma: 

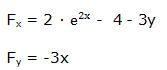
Luego:

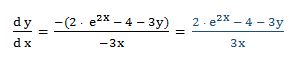
6.- Dada la función: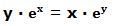  

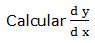
Escribimos la función en la forma: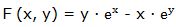 

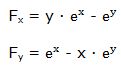
Luego:

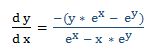
7.- Dada la función: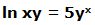  

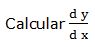
Escribimos la función en la forma: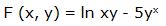 

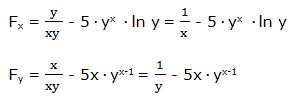
Luego:

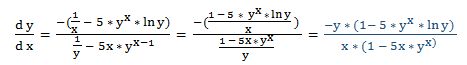
 8.- Dada la función: 5 · cos y = 6 · sen x

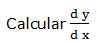
Escribimos la función en la forma: F (x, y) = 5 · cos y - 6 · sen x

F_x = 6 · cos x

F_y = 5 · (-sen y)

Luego:

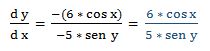
 9.- Dada la función: sen xy = cos xy

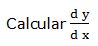
Escribimos la función en la forma: F (x, y) = sen xy - cos xy

F_x = y · cos xy + y · sen xy

F_y = x · cos xy + x · sen xy

Luego:

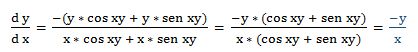
10.- Dada la función: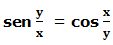 

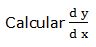
Escribimos la función en la forma: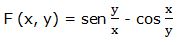 

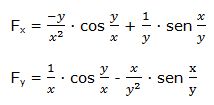
Luego:

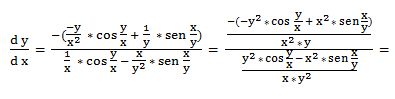
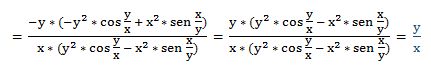
11.- Dada la función: 4x^y = 3y^x

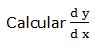
Escribimos la función en la forma: F (x, y) = 4x^y - 3y^x

F_x = 4y · x^y-1 - 3y^x ·ln y

F_y = 4x^y ·ln x-3x · y^x-1

Luego:

 
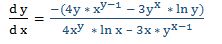
CASO DE DOS VARIABLES INDEPENDIENTES

1.- Dada la función: 5x²y- 3xy² = 7xyz

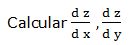
Escribimos la función en la forma: F (x, y, z) = 5x²y- 3xy² - 7xyz

F_x = 10xy- 3y² - 7yz

F_y = 5x² - 6xy- 7xz

F_z = -7xy

Luego:

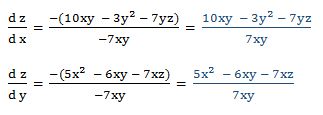
2.- Dada la función: ln 3xy + ln 2xz= ln 5yz

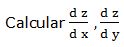
Escribimos la función en la forma: F (x, y, z) = ln 3xy + ln 2xz- ln 5yz

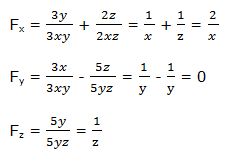
Luego:

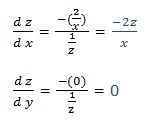
3.- Dada la función: sen xyz = cos xyz

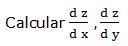
Escribimos la función en la forma: F (x, y, z) = sen xyz - cos xyz

F_x = yz · cos xyz - yz · sen xyz

F_y = xz · cos xyz - xz · sen xyz

F_z = xy · cos xyz - xy · sen xyz

Luego:

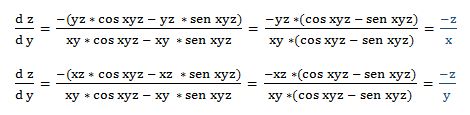
4.- Dada la función: 3x^yz + 5y^xz = 8z^xy

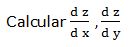
Escribimos la función en la forma: F (x, y, z) = 3x^yz + 5y^xz - 8z^xy

F_x = 3yz · x^yz-1 + 5z · y^xz · ln y - 8y · z^xy · ln z

F_y = 3z · x^yz · ln x + 5xz · y^xz-1 – 8x · z^xy · ln z

F_z = 3y · x^yz · ln x + 5x · y^xz · ln y – 8xy · z^xy-1

Luego: