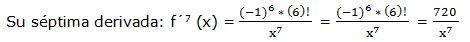Derivadas sucesivas

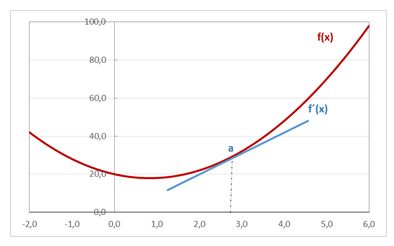
Cuando derivamos una función obtenemos la primera derivada f´(x)

Si derivamos esta primera derivada obtenemos la segunda derivada f´´(x)

Si derivamos esta segunda derivada obtenemos la tercera derivada f´´´(x)

Si derivamos esta tercera derivada obtenemos la cuarta derivada f´´´´(x)

Y así sucesivamente.

Las derivadas segunda y sucesivas de f(x) se denominan derivadas de orden superior de f(x).

Ejemplo:

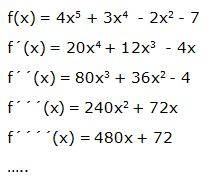
Veamos otro ejemplo:

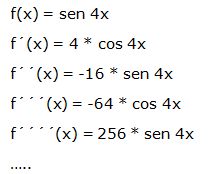
Algunas funciones se pueden derivar un número limitado de veces:

El primer ejemplo que hemos visto:

Su derivada quinta sería: f´´´´´(x) = 480

Y su derivada sexta: f´⁶ (x) = 0

Mientras que otras funciones se pueden derivar infinitas veces, como el segundo ejemplo que hemos visto.

Derivadas enésima

En algunas funciones se puede deducir una fórmula que nos permite calcular cualquier derivada sucesiva. A esta fórmula se le denomina derivada enésima f´ⁿ (x).

Veamos un ejemplo:

f(x) = e^2x

Su primera derivada: f´(x) = 2 * e^2x

Su segunda derivada: f´´(x) = 4 * e^2x

Su tercera derivada: f´´´(x) = 8 * e^2x

^…..

Su derivada enésima es: f´ⁿ (x) = 2ⁿ * e^2x

Esta fórmula nos permite calcular cualquier derivada sucesiva:

Por ejemplo:

Su sexta derivada: f´⁶ (x) = 2⁶ * e^2x

Veamos otro ejemplo:

f(x) = ln x

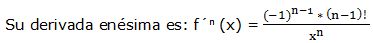
Esta fórmula nos permite calcular cualquier derivada sucesiva:

Por ejemplo: