Derivada de un logaritmo

Hay dos formas de definirla:

Es igual al producto de dos factores: la derivada del argumento “w” dividida por el argumento multiplicado por el logaritmo en base “b” del número “e”.

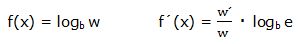
También se puede definir: la derivada del argumento “w” dividido por el argumento multiplicado por uno dividido por el logaritmo neperiano de la base “b”.

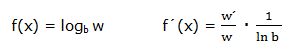
Para resolver las derivadas de logaritmos puede ser útil en algunos casos descomponerlos utilizando las propiedades de los logaritmos. A título de ejemplo en algunos ejemplos que veremos a continuación utilizaremos dicha técnica.

Ejemplo:

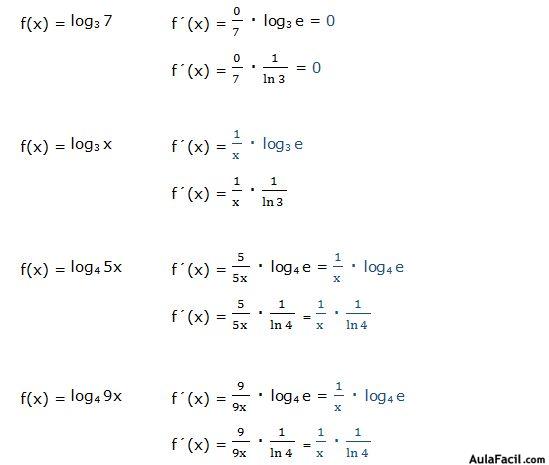
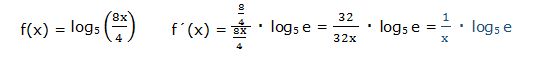
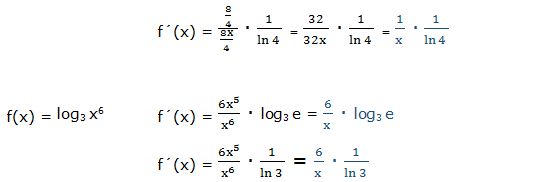
En el cálculo de la derivada de un logaritmo puede ser muy útil aplicar las propiedades de los logaritmos. Por ejemplo, en el caso anterior podríamos haber operado de la siguiente manera:

f(x) = log₃ x⁶ ₌ 6 · log₃ x

Luego:

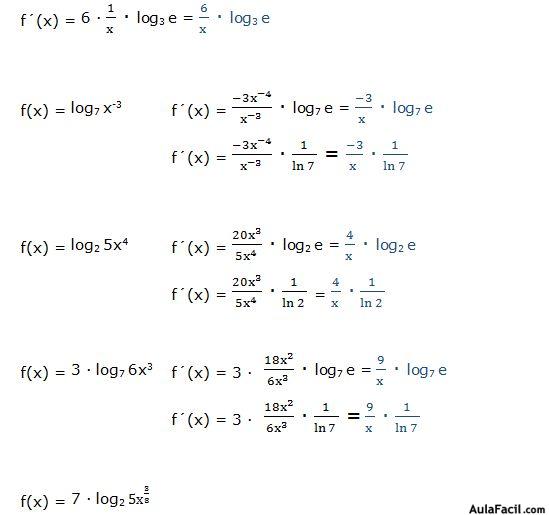
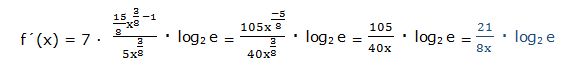
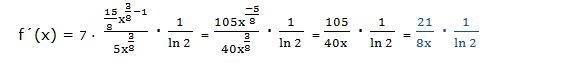
Esta derivada hubiera sido más fácil resolverla aplicando las propiedades de los logaritmos:

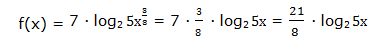
Luego:

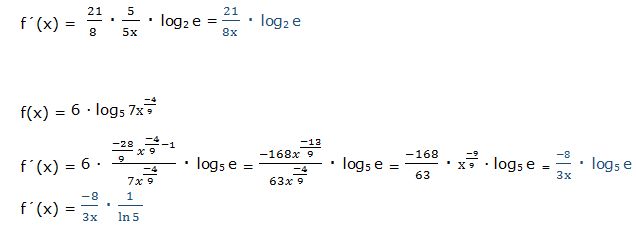
Aplicando las propiedades de los logaritmos:

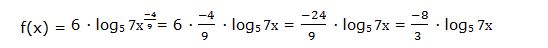
Luego:

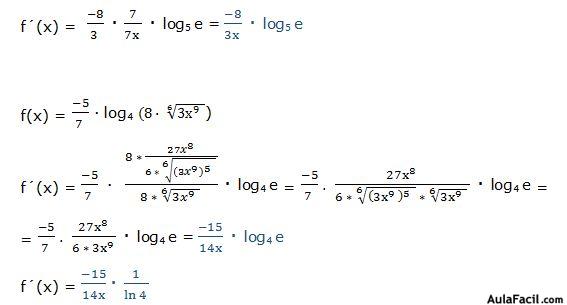
Se podría resolver aplicando las propiedades de los logaritmos:

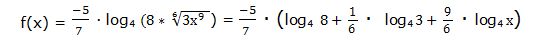
Luego:

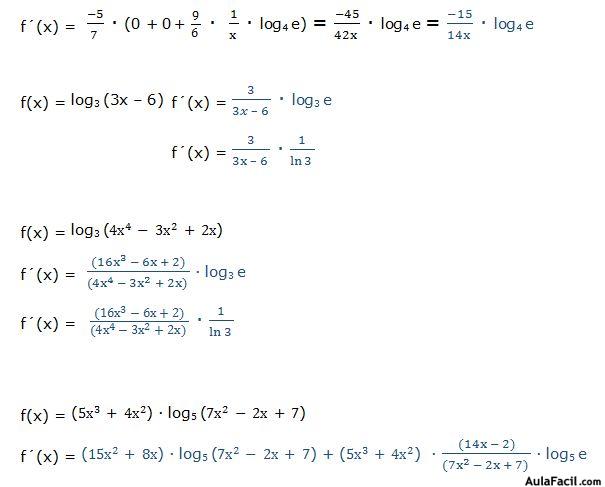
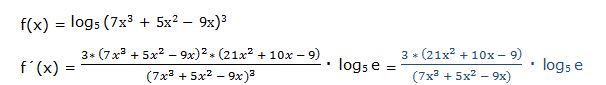
También se podría resolver aplicando las propiedades de los logaritmos:

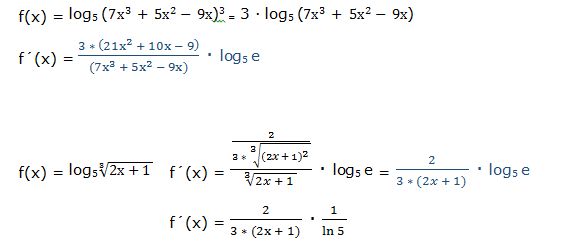
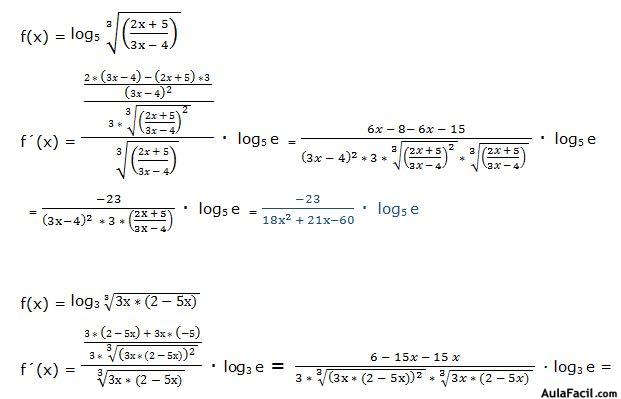
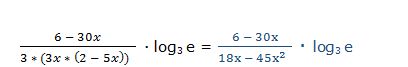
También podemos resolverlo aplicando las propiedades de los logaritmos:

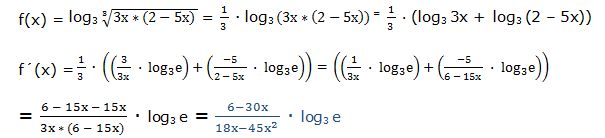
Hemos obtenido el mismo resultado.