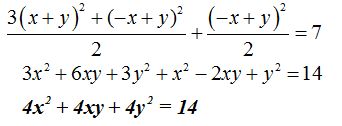Única ecuación general para las cónicas
Podemos decir que la ecuación general única, válida para todas las cónicas cuyos ejes son paralelos a los de sus coordenadas podemos escribirla:
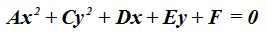
Es normal que digas que no comprendes la validez de esta ecuación. Posiblemente extrañarás que falta el coeficiente B. No es que se nos haya olvidado.
Cuando hemos estudiado las cónicas nunca nos hemos referido a ecuaciones procedentes de un giro de una rotación de los ejes de coordenadas:
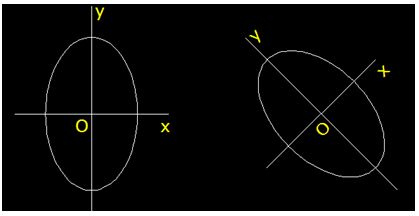
Como ves, en esta elipse hemos dado un giro de 45º en sentido contrario a la marcha de las agujas de un reloj.
Hasta ahora habíamos trasladado los ejes de coordenadas a otros puntos del plano, pero nunca nos habíamos referido a la rotación de dichos ejes.
En los casos en que calculamos la ecuación de una cónica tras una rotación, aparece el término Bxy.
Vamos a estudiar el modo de calcular los valores de las coordenadas de un punto P(x,y) después de haber efectuado una rotación de α grados.
Representamos gráficamente cuanto decimos:
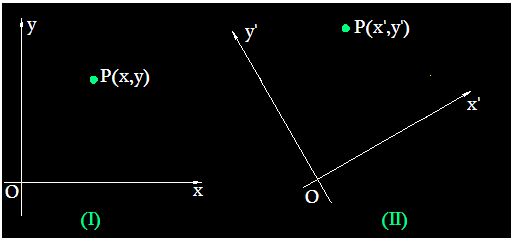
En la figura (I) tenemos un punto P con sus coordenadas en el origen.
En la figura (II) hemos girado 30º el eje de coordenadas en sentido contrario a la marcha de las agujas de un reloj. La posición del punto P ha variado y sus coordenadas también.
Ahora nos referimos a x’ e y’.
Para calcular el valor de las nuevas coordenadas x’ e y’ debes fijarte el la figura siguiente:
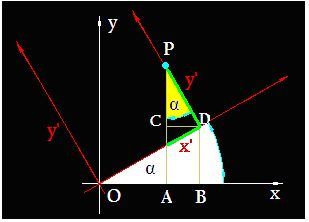
Los ángulos α son iguales por tener sus lados perpendiculares.
Las coordenadas del punto P(x,y) podemos escribirlas:
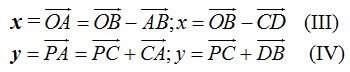
Si hallamos el coseno del ángulo α (fondo blanco) teniendo en cuenta que el radio o hipotenusa vale x’tendremos:
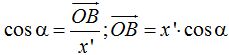
Tomamos el otro ángulo α (fondo amarillo), el seno de éste ángulo donde la hipotenusa vale y’ podemos escribir:
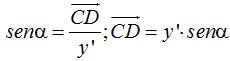
Estos valores los sustituimos en (III):
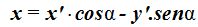
Ahora hacemos lo mismo con lo que tenemos en (IV).
El valor de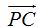 
(ángulo α fondo amarillo) equivale a:
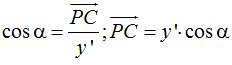
El valor de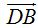 
(ángulo α fondo blanco) equivale a:
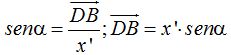
Estos valores los sustituimos en (IV):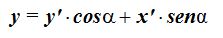 
Ordenando (más fácil de recordar) los valores de x e y después de un giro de α grados equivalen a:
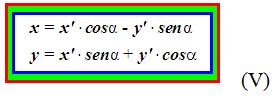
A partir de aquí, hemos de presentar la nueva ecuación tras el giro, en este caso, de una parábola.
El término Bxy en la ecuación general de una cónica:
Cuando efectuamos un giro de una cónica, se produce la aparición de un término cuya parte literal es xy.
Esto lo comprobamos cuando calculamos la ecuación de la cónica tras una rotación como puedes comprobar a continuación.
26.48 La ecuación de una parábola es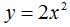 
. Escribe esta ecuación después de girar 30º.
Respuesta: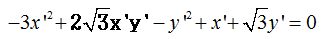 
Solución
Sabemos por lo estudiado en Trigonometría que:
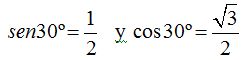
Sustituyendo estos valores en (V):
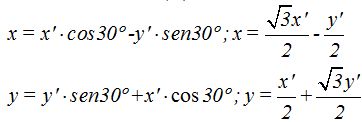
Estos valores de x e y que han sido alterados por el giro, los sustituyo en la ecuación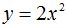 
y el resultado que obtenga corresponderá a esta parábola tras haber efectuado un giro de 30º:
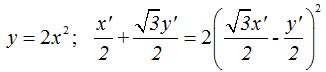
Dejando todos los términos en el primer miembro:
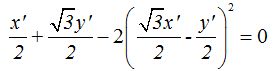
Haciendo operaciones:
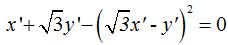
Elevando al cuadrado:
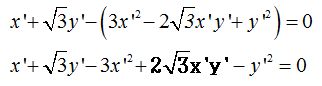
Ordenamos:
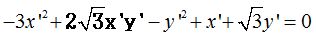
Comprobación gráfica:
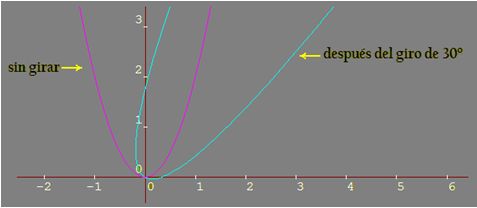
Compruebo en la ecuación obtenida tras el giro de 30º la aparición del término cuya parte literal es xy que se produce tras una rotación en las cónicas (excepto la circunferencia).
La ecuación general que contempla giros y traslaciones la escribimos:
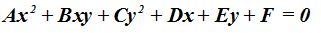
26.49 La ecuación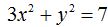 
corresponde a la elipse que ves en la figura siguiente:
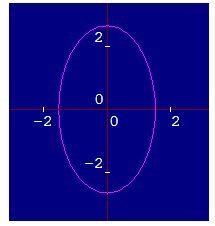
Comprueba el resultado.
Respuesta: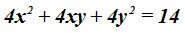 
Comprobación gráfica:
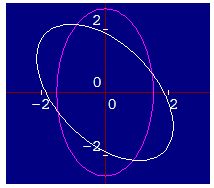
Solución
Sabemos por lo estudiado en Trigonometría que el seno y coseno del ángulo de 45º valen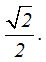 
Podemos escribir:
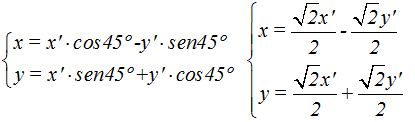
Resolvemos el sistema (método de reducción):
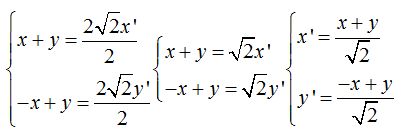
Sustituimos los valores hallados en la ecuación que nos han propuesto y haciendo operaciones obtenemos:
