Zona Horaria y Zona Esférica
Lo que has estudiado respecto al huso horario no se cumple en la práctica.
Cuando perteneciendo a diferentes husos horarios, por razones de límites de fronteras de países, regiones, convenios, compromisos, etc., deciden tener la misma hora, nos referimos a la zona horaria, por ejemplo, en la UE (Unión Europea) donde se ha tomado la misma hora para los países que pertenecen a esta organización que de momento se excluyen a Portugal y Reino Unido Con el fin de aclararnos un poco observa la figura correspondiente del contenido siguiente:
Mapa plano con los usos horarios:
Tienes a continuación un mapa con los husos y zonas horarias.
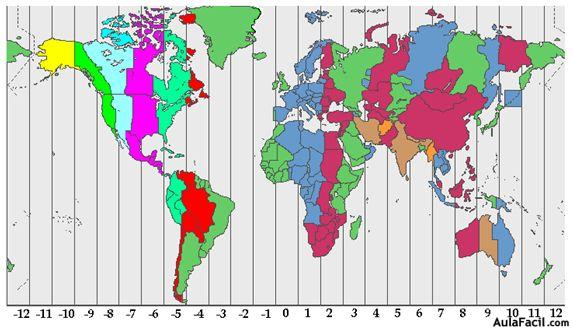
Los países que ves del mismo color y en sentido vertical corresponden incluidos en uno, dos o más husos horarios corresponden a la misma zona horaria.
15(4).18 Cuando en España son las 4 de la tarde ¿qué hora es la ciudad de Sydney (costa Este de Australia)?
Respuesta: la 1 de la mañana del día siguiente
Solución
Si nos fijamos en la figura última, vemos que Sydney se encuentra 9 husos a la derecha de España lo que corresponde a 9 horas más en la ciudad australiana, es decir, la 1 de la mañana del día siguiente.
15(4).19 Cuando en España son las 2 de la madrugada ¿qué hora es la capital de Chile, Santiago?
Respuesta: las 8 de la tarde de ayer
Solución
Si nos fijamos en la figura última, vemos que Santiago se encuentra 6 husos a izquierda, es decir, 6 horas menos, que equivalen a las 8 de la tarde del día anterior en Santiago.
15(4).20 Cuando en España son las 12 del mediodía qué hora es en Tokio, capital de Japón?
Respuesta: las 8 de la tarde del mismo día
Solución
Japón se encuentra 8 husos horarios a la derecha de nuestra zona horaria, por lo tanto, serán las 8 de la tarde del mismo día.
15(4).21 Cuando en España son las 10 de la mañana ¿qué hora es en Reykiavik, capital de Islandia?
Respuesta: las 9 de la mañana del mismo día
ZONA ESFÉRICA.
En el Tema 15(3) recordarás que estudiamos la zona esférica como la intersección de dos planos paralelos con una esfera.
Deducir el área de la zona esférica no es una tarea sencilla.
Sirviéndonos de los grandes genios como Arquímedes, 250 años antes de Cristo nos dijo que la superficie de una zona esférica que corresponde a una esfera de radio R y una distancia h entre los dos planos paralelos que cortan a la esfera, es igual a la superficie de un cilindro con el mismo radio R y una altura h.
Veamos la figura siguiente:
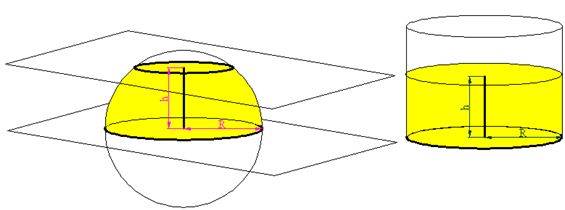
Tienes a la izquierda (color amarillo) la sección de esfera que nos ha quedado después que le han cortado dos planos paralelos y perpendiculares a su eje vertical.
A la derecha un cilindro que tiene el mismo radio y misma altura y en amarillo la misma superficie correspondiente al área lateral del cilindro de radio R y altura h.
Calcular la superficie lateral en el cilindro es muy sencillo, sabemos que equivale a multiplicar la longitud de la base por la altura.
Como la base es una circunferencia de radio R y la altura h, el área será:
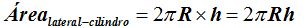
y el área de la zona esférica de radio R y altura entre los planos paralelos h será la misma, es decir 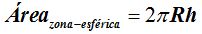
Puedes comprobar tomando una esfera que tenga una superficie áspera de modo que se fije la cuerda a medida que la vas colocando alrededor de la misma comenzando por el lugar que desees como puedes ver en la figura siguiente:
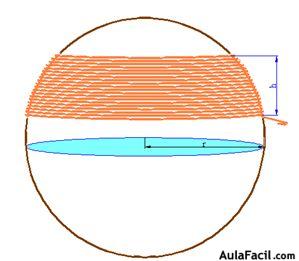
Una vez que colocada la cuerda sobre la superficie esférica y cuando hayas conseguido una altura de 3 ó 4 cm., retiras la cuerda utilizada y en un tubo o recipiente cilíndrico del mismo radio que la esfera anterior, la vuelves a colocar, como ves en la figura siguiente:
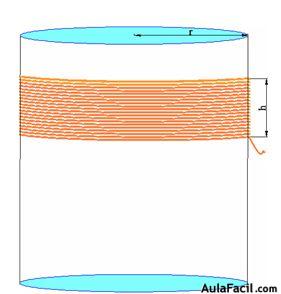
y comprobarás que finalizada la colocación de la misma, habrás conseguido, en el cilindro, la misma altura por lo que podemos afirmar que las dos superficies, en la esfera y en el cilindro son iguales.
De esta observación debida a Arquímedes nos es fácil calcular el área de una zona esférica, sirviéndonos del área lateral del cilindro.
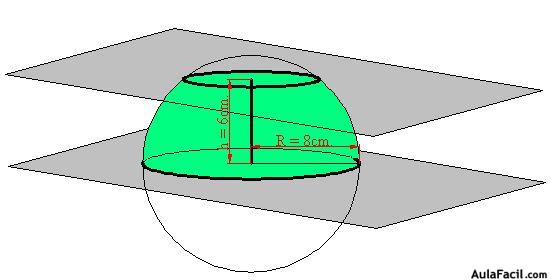
15(4).22 Calcula el área de una zona esférica de 6 cm., de altura. El radio de la esfera vale 8 cm. Dibuja la figura.
Respuesta: 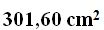
La figura podría ser: