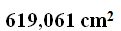Áreas de los Prismas Regulares. (Continuación)
El desarrollo de un prisma regular cuya base es un pentágono es:
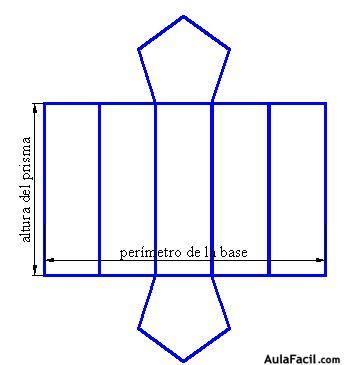
El área lateral es igual al perímetro de la base (la suma de las medidas de los 5 lados del pentágono) por la altura del prisma o arista lateral.
Llamamos P al perímetro
h a la altura
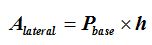
El área total igual al área lateral más el área de las dos bases que son 2 pentágonos iguales.
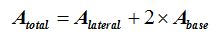
El problema surge en el pentágono cuando hemos de calcular el área de un triángulo isósceles, de los 5 en que dividimos al mismo tal como lo estudiamos en el Tema 15(3)al calcular el volumen del dodecaedro.
Tomando como longitud del lado del pentágono 1 y haciendo uso de 
tal como quedó demostrado, cada uno de los lados iguales del triángulo isósceles vale 0,8506, de donde la altura vale:
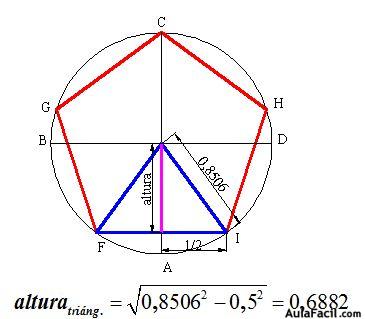
El área de un triángulo será:
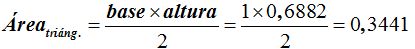
y el área de los 5 triángulos:
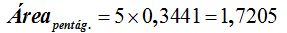
Este resultado es válido para cuando el valor del lado sea 1, si se trata de un valor a, lo multiplicaremos por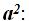 
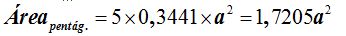
El área total siendo a el lado del pentágono y h la altura del prisma será:
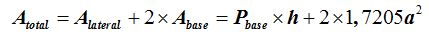
15(4).9 Un prisma de base pentagonal de 3 cm. de lado y una altura de 10 cm., ¿qué superficie total tiene?
Respuesta: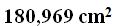 
Solución
Sustituyendo directamente los datos conocidos en la fórmula obtenida:
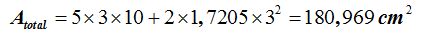
El desarrollo de un prisma regular cuya base es un hexágono es:
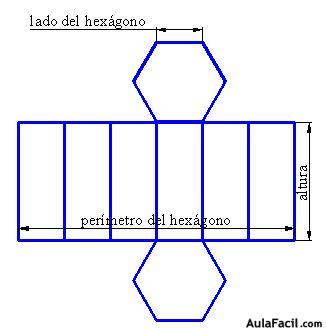
El área lateral es igual al perímetro de la base (la suma de las medidas de los 6 lados del hexágono) por la altura del prisma o arista lateral.
Llamamos P al perímetro
h a la altura
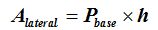
El área total igual al área lateral más el área de las dos bases que son 2 hexágonos iguales.
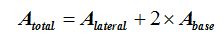
15(4).10 Un prisma de base hexagonal de 3 cm. de lado y una altura de 10 cm., ¿qué superficie total tiene?
Respuesta: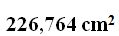 
Solución
Calculamos el área lateral:
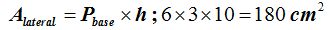
Un hexágono contiene 6 triángulos equiláteros: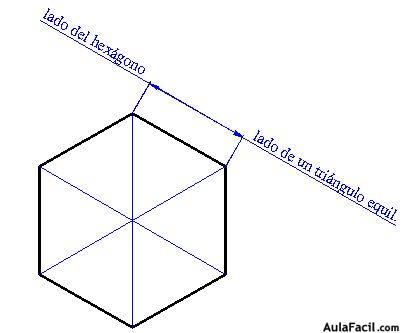
Calculamos la altura de un triángulo:
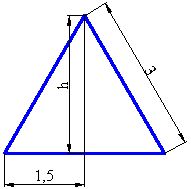
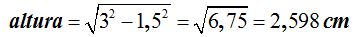
El área de la base será 6 veces el de un triángulo:
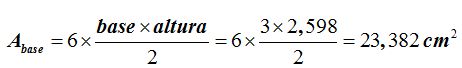
El área total será:
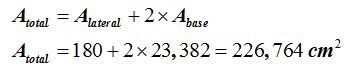
15(4).11 Un prisma de base hexagonal de 6 cm. de lado y una altura de 12 cm., ¿qué superficie total tiene?
Respuesta: 
