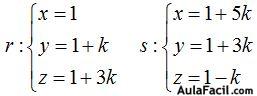Soluciones
24.40 Una recta que sea paralela a un plano, su vector director tendrá que ser perpendicular al vector normal del plano.
El vector normal del plano es 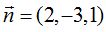
De los infinitos vectores perpendiculares a 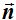 uno podría ser:
uno podría ser: 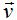 = (1,1,1) ¿Por qué?
= (1,1,1) ¿Por qué?
Porque sabemos que el producto escalar de 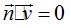
Si multiplicas 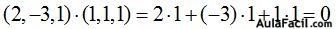
Otro vector perpendicular a 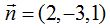 puede ser
puede ser 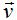 = (0,13)
= (0,13)
Tomamos a este último como vector de la recta r.
Ahora nos falta conocer un vector, correspondiente a la recta s que tiene que ser perpendicular a 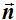 y
y 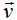 , es decir:
, es decir:
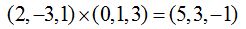
Ya tenemos los dos vectores y vemos que nos falta un punto exterior al plano para resolver el problema.
De los infinitos puntos no pertenecientes al plano tomamos el punto P(1,1,1). Sabemos que este punto no se encuentra en el plano 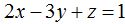 porque al sustituir x, y, z por los valores 1, 1, 1 hallamos 0 por respuesta en lugar de 1.Las rectas en forma paramétrica las escribimos:
porque al sustituir x, y, z por los valores 1, 1, 1 hallamos 0 por respuesta en lugar de 1.Las rectas en forma paramétrica las escribimos: