Soluciones
24.35 Observamos en la ecuación de la recta un vector director:
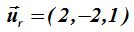
Como el plano contiene a la recta,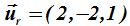 
será paralelo a este vector director y también contendrá al punto 
.
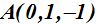El punto P(1, 2, 3) y el punto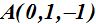 
se encuentran en el plano de donde podemos calcular el vector 
.
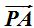El vector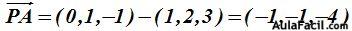 
Un punto cualquiera del plano tendrá como componentes: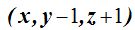 
Tenemos los datos suficientes para dar respuesta al enunciado de este problema:
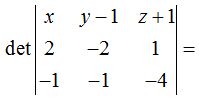
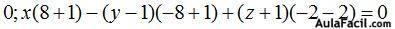
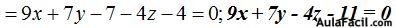
24.36 En el ejercicio 24.31 calculamos los planos bisectores:
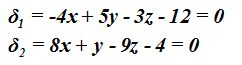
Las componentes de las normales son 
El ángulo, llamemos α, entre dos planos nos viene dado por:
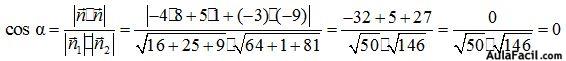
Hubiese bastado con multiplicar, escalarmente, las componentes de los vectores normales (es decir, como lo tenemos en el numerador de la expresión anterior).
Como sabemos que cos 90º vale 0 significa que los planos bisectores son perpendiculares (EL ARCO CUYO COSENO VALE 0 CORRESPONDE A 90º).
Respuesta: 90º los planos bisectores son perpendiculares.
24.37 El vector director de la recta r según los datos que nos proporciona el enunciado del problema son: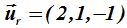 
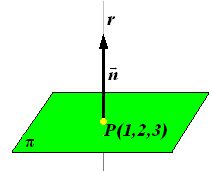
Por otro lado, esas componentes corresponden también a la normal del plano 
: 
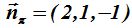
Sabemos que en la ecuación general del plano: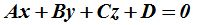 
Los coeficientes: A, B, C corresponden a las componentes de la normal.
La ecuación del plano, a falta de conocer el valor de D, es:
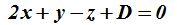
El punto P(1, 2, 3) corresponde también al plano. Sustituimos en: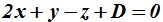 
estos valores y hallamos el de D:
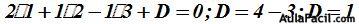
La ecuación del plano es: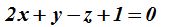 
24.38 Primero resolvemos el sistema y para ello a la variable z le damos el valor k porque vamos a calcular la ecuación de la recta en la forma paramétrica.
z = k
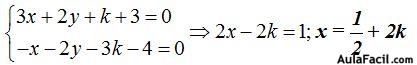
Calculamos el valor de y sustituyendo los valores conocidos en la 2ª ecuación:
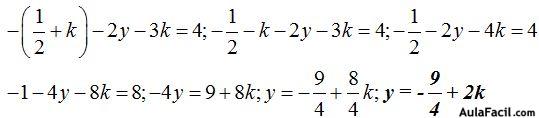
Tenemos los parámetros del punto y del vector director:
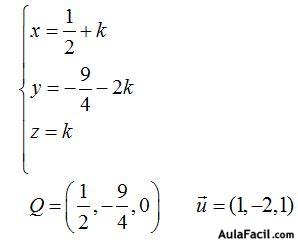
La distancia de un punto 
a la recta:
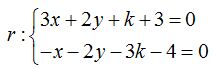
viene dada por: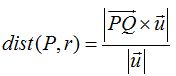 
El vector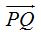 
tiene como componentes:
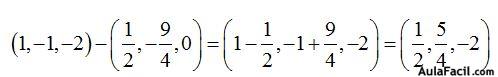
Calculamos el valor del numerador: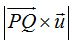 
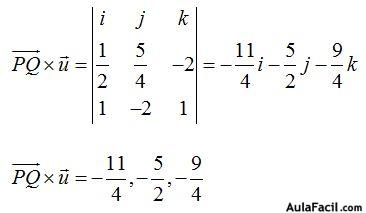
Ahora hallamos el valor del módulo del numerador:
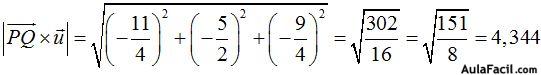
Calculamos el valor del módulo del denominador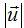 
:
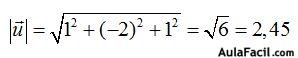
La distancia pedida será:
