Cocientes notables (generalización)
Cociente de la diferencia de potencias iguales entre la diferencia de sus bases.
La diferencia de dos potencias de exponentes iguales, ya sea pares o impares, siempre es divisible entre la diferencia de sus bases.
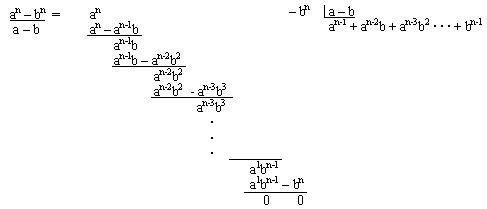
Como se demuestra en la división mostrada no importa que exponente sea usado el resultado siempre será exacto.
Para escribir el resultado se siguen los siguientes pasos:
Existirá un número de términos igual al exponente de los términos del dividendo y todos serán positivos.
En cada término se multiplicara el término de la izquierda por el término de la derecha de la expresión dada.
En el primer término el factor de la izquierda tendrá un exponente igual al de el dividendo disminuido en uno, y el factor de la izquierda tendrá un exponente de cero.
Para los exponentes de los siguientes términos, en el caso del término de la izquierda irán disminuyendo en una unidad, y los del término de la derecha irán aumentando también en una unidad (si se suman los exponentes de los dos términos siempre será igual a n-1)
Cuando el exponente del termino de la derecha sea igual a n-1 damos por terminada la respuesta.
Ejemplos:
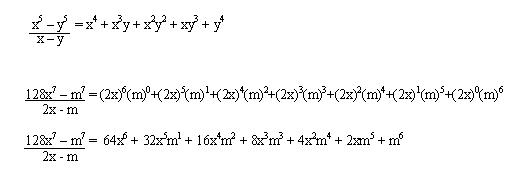
De la misma manera que se demuestra y trabaja este cociente se demuestran otros que simplemente resumiremos a continuación:
Suma de potencias iguales impares entre la suma de sus bases
La suma de potencias de exponentes iguales impares siempre es divisible exactamente entre la suma de sus bases. Se estructura igual que el anterior con la siguiente diferencia en el paso uno
- El primer factor del resultado será positivo el segundo negativo y de esta manera seguirán alternándose hasta terminar el polinomio.
Ejemplos:
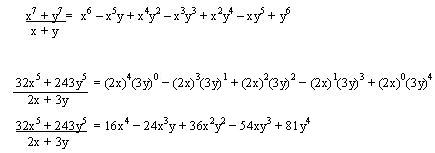
Diferencia de potencias iguales pares entre la suma de sus bases
La diferencia de potencias de exponentes iguales pares siempre es divisible exactamente entre la suma de sus bases. Se estructura exactamente igual que el anterior sin diferencias.
Ejemplos:
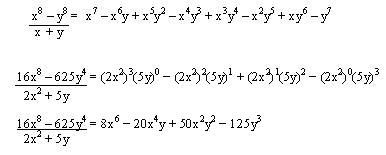
Es necesario hacer mención que, si tenemos una suma de potencias iguales pares nunca será divisible exactamente entre la suma de sus bases, tampoco lo será la diferencia de potencias iguales impares si se divide si se divide entre la suma de sus bases.

