Semejanzas

Figuras semejantes son aquellas que son exactamente iguales en forma pero que se diferencian en el tamaño.
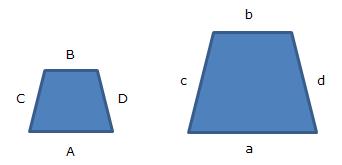
Sus lados son proporcionales y sus ángulos son iguales.
Razón de semejanza
Los lados guardan uno a uno la misma proporción.
A y a
B y b
C y c
D y d
La proporción entre ellos es la misma. A esta proporción se le denomina “razón de semejanza”
Veamos un ejemplo:
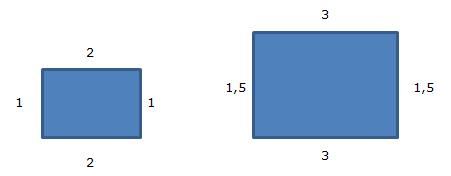
Los lados horizontales miden 2 y 3 respectivamente, la proporción entre ellos es:
2 / 3 = 0,66
Los lados verticales miden 1 y 1,5 respectivamente, la proporción entre ellos es:
1 / 1,5 = 0,66
Por lo tanto, la razón de semejanza de estas dos figuras es 0,66.


